Forces 50N and 80N act on a body as shown in the diagram....
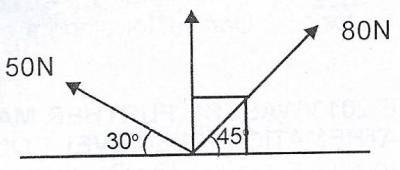
Forces 50N and 80N act on a body as shown in the diagram. Find, correct to the nearest whole number, the horizontal component of the resultant force.
13N
43N
57N
95N
Correct answer is A
Given a force F, the horizontal component = \(F\cos \theta\)
R = \(-50\cos 30 + 80\cos 45\)
= \(-50(\frac{\sqrt{3}}{2}) + 80(\frac{\sqrt{2}}{2})\)
= \( -25\sqrt{3} + 40\sqrt{2} = -43.30 + 56.67 \)
= \(13.37N \approxeq 13N\)
Similar Questions
A particle is acted upon by forces F = (10N, 060º), P = (15N, 120º) and Q = (12N, 200º...
If \(\begin{pmatrix} 2 & 1 \\ 4 & 3 \end{pmatrix}\)\(\begin{pmatrix}...
Simplify \(2\log_{3} 8 - 3\log_{3} 2\)...
Solve the inequality \(x^{2} - 2x \geq 3\)...
If cos x = -0.7133, find the values of x between 0\(^o\) and 360\(^o\) ...
Express \(\log \frac{1}{8} + \log \frac{1}{2}\) in terms of \(\log 2\)...
Find the variance of 1, 2, 0, -3, 5, -2, 4....
Find the coefficient of \(x^{4}\) in the expansion of \((1-2x)^{6}\)...