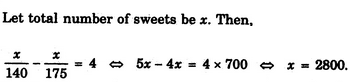Numerical Reasoning Questions and Answers
Numerical Reasoning test is a set of multiple choice questions and answers that assesses your ability to deal with numbers quickly and accurately. This test contains questions that assess your knowledge of concepts such as arithmetics, percentages, ratios, averages, simplification, algebra, logarithm etc.
Practise with our Numerical Resoning test questions to help you know what to expect, improve your speed and confidence and be really prepared for the actual test.