Solve the following quadratic inequality: \(x^2 - x\) - 4 ≤ 2
\(-3 < x < 2\)
\(-2 ≤ x ≤ 3\)
\(x ≤ -2, x ≤ 3\)
\(-2 < x < 3\)
Correct answer is B
\(x^2 - x - 4 ≤ 2\)
Subtract two from both sides to rewrite it in the quadratic standard form:
= \(x^2 - x - 4 - 2 ≤ 2 - 2\)
= \(x^2 - x - 6 ≤ 0\)
Now set it = 0 and factor and solve like normal.
= \(x^2 - x\) - 6=0
= \((x - 3)(x + 2)\)=0
\(x\) + 2 = 0 or \(x\) - 3 = 0
\(x\) = -2 or \(x\) = 3
So the two zeros are -2 and 3, and will mark the boundaries of our answer interval. To find out if the interval is between -2 and 3, or on either side, we simply take a test point between -2 and 3 (for instance, \(x\) = 0) and evaluate the original inequality.
= \(x2 - x - 4 ≤ 2\)
= \((0)^2 - (0) - 4 ≤ 2\)
= \(0 - 0 - 4 ≤ 2\)
\(−4 ≤ 2\)
Since the above is a true statement, we know that the solution interval is between -2 and 3, the same region where we picked our test point. Since the original inequality was less than or equal, we include the endpoints.
∴ \(-2 ≤ x ≤ 3.\)
Let a binary operation '*' be defined on a set A. The operation will be commutative if
a*b = b*a
(a*b)*c = a*(b*c)
(b ο c)*a = (b*a) ο (c*a)
None of the above
Correct answer is A
A binary operation '*' defined on a set A is said to be commutative only if a*b=b*a, ∀a, b∈A. If (a*b)*c=a*(b*c), then the operation is said to associative ∀ a, b∈ A. If (b ο c)*a=(b*a) ο (c*a), then the operation is said to be distributive ∀ a, b, c ∈ A.
If \(-2x^3 + 6x^2 + 17x\) - 21 is divided by \((x + 1)\), then the remainder is
32
30
-30
-32
Correct answer is C
Let \(p(x) = -2x^3 + 6x^2 + 17x - 21\)
Using the remainder theorem
Let \(x + 1 = 0\)
∴ \(x = -1\)
Since, \((x + 1)\) divides \(p(x)\), then, remainder will be p(-1)
⇒ p(-1) = -2(-1)\(^3 + 6(-1)^2\) + 17(-1) - 21
∴ p(-1) = -30
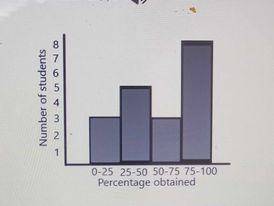
How many students scored at least 25%
16
19
3
8
Correct answer is A
Number of students who scored atleast 25% = 5 + 3 + 8 = 16
\(\begin {bmatrix} 2 & 1\\-^1/_2 & -^1/_2 \end {bmatrix}\)
\(\begin {bmatrix} 0 & 1\\^1/_2 & ^1/_2 \end {bmatrix}\)
\(\begin {bmatrix} 2 & 1\\0 & -1 \end {bmatrix}\)
\(\begin {bmatrix} 2 & 1\\^1/_2 & -2 \end {bmatrix}\)
Correct answer is B
Let A = \(\begin {bmatrix} a & b\\ c & d \end {bmatrix}\)
i.e \(\begin{bmatrix} a & b\\c & d \end{bmatrix}\) \(\begin{bmatrix} 0 & 1\\2 & -1 \end{bmatrix}\) = \(\begin{bmatrix} 2 & -1\\1 & 0 \end{bmatrix}\)
\(\implies \begin {bmatrix} a(0) + b(2) & a(1) + b(-1)\\ c(0) + d(2) & c(1) + d(-1)\end {bmatrix}\) = \(\begin {bmatrix} 2 & -1\\ 1 & 0 \end {bmatrix}\)
\(\implies \begin {bmatrix} 2b & a - b\\2d & c - d\end {bmatrix}\) = \(\begin {bmatrix} 2 & -1\\ 1 & 0 \end {bmatrix}\)
By comparing
2b = 2
a - b = -1
2d = 1 and
c - d = 0
∴ b = \(^2/_2\) = 1
a - b = -1
⇒ a - 1 = -1
∴ a = 0
∴ d = \(^1/_2\)
⇒ c = d
∴ c = \(^1/_2\)
∴The matrice A = \(\begin {bmatrix} 0 & 1\\^1/_2 & ^1/_2 \end {bmatrix}\)
JAMB Subjects
Aptitude Tests