JAMB Physics Past Questions & Answers - Page 10

A=0.8m; f=16Hz; v=20 $ms^-1$; k=?

v = fλ

λ =1.25m

= k= $\frac{2π}{λ}$ =$\frac{2 × 3.142}{1.25}$
 
 k=  5m ( to 1 s.f)

 

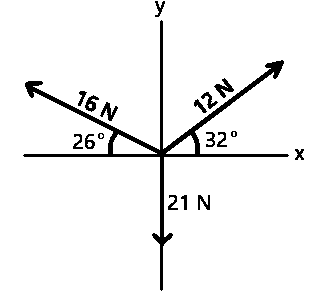
Fx= 12cos32°-16cos26°    =    -4.20N    (right is taken +ve and left is taken -ve)

Fy=12sin32°+16sin26°-21 = -7.63N  (up is taken +ve and down is taken -ve)

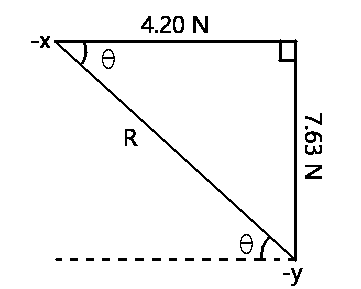
$R^2$= 4.202+7.632

⇒$R^2$ = 75.86

⇒ R=√75.86

∴R = 8.71 N

tan θ=$\frac{opp}{adj}$

⇒tan θ=$\frac{7.63}{4.20}$

⇒tan θ =1.8095

⇒ θ = $tan^-1$ (1.8095)

   θ = 61°

∴The angle of the resultant force with the x-axis is 61°

     Let the original length L=xm

      ;New length =( x -3 ) m

       $T_1$ = 5.77s; $T_2$ = 4.60s,  

       $T^2$ α  L

       ⇒$T_2) = kL  where K is constant        ⇒K = \(\frac{T^2_1}{L_1}$ = $\frac{T^2_2}{L_2}$

      ⇒$\frac{5.77^2}{x}$  = $\frac{4.60^2}{x-3}$

      ⇒ $\frac{33.29}{x}$  = $\frac{4.60^2}{x-3}$

      ⇒ 33.29(x-3)  = 21.16x
        
      ⇒ 33.29x - 99.87 =21.16x

      ⇒12.13x = 99.87
     
      ;x =$\frac{99.87}{12.13}$  = 8.23m
    
      New length of the pendulum 
     
      =x-3 = 8.23-3
   
      =5.23m

     

n=1.458, c=$3.00 ×10^8 ms^-1$ ,λo = 589nm;  f=?

Speed of light in a medium (v)=$\frac{c}{n}$  where n is the refractive index of the medium

⇒λn=$\frac{589}{1.458}$ = 404nm

  v=fλ
  
⇒f=$\frac{v}{λ}$ 

=$\frac{2.06×10^8}{404×10^-9}$ $1nano=10^{-9}$

∴f=$5.09×10^{14}$ Hz

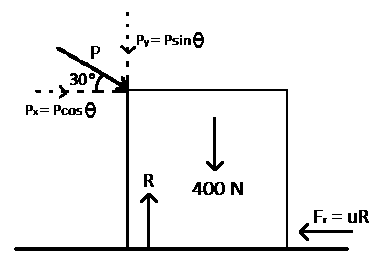
W = 400 N; P = 100 N; θ = 30o; μ = ?

Frictional force (Fr) = μR (where R is the normal reaction)

The forces acting along the horizontal direction are Fr and Px

∴ Pcos 30° - Fr = ma (Pcos 30° is acting in the +ve x-axis while Fr in the -ve x-axis)

⇒ 100cos 30° - μR = ma

Since the box is moving at constant speed, its acceleration is zero

⇒ 100cos 30° - μR = 0

⇒ 100cos 30o = μR ----- (i)

The forces acting in the vertical direction are W, Py and R

∴ R - Psin 30° - W = 0 (R is acting upward (+ve) while Py and W are acting downward (-ve) and they are at equilibrium)

⇒ R - 100sin 30° - 400 = 0

⇒ R = 100sin 30° + 400

⇒ R = 50 + 400 = 450 N

From equation (i)

⇒ 100cos 30° = 450μ

⇒μ=100cos30°

  N = $\frac{100cos30°}{450}$

        = μ = 0.19