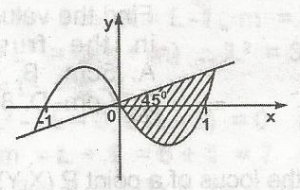
the shaded portion in the graph is represented by
y + x - x \(\leq\) 0, y - x \(\leq\) 0
y - x + x, 3 \(\leq\) 0, y - x \(\geq\) 0
y + x - 3 \(\geq\) 0, y + x \(\leq\) 0
y - x + x3 \(\geq\) 0, y + x \(\leq\) 0
Correct answer is C
No explanation has been provided for this answer.

59.4%
50.0%
41.7%
25.0%
Correct answer is C
\(\begin{array}{c|c} x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline f & 1 & 9 & 4 & 7 & 10 & 8 & 7 & 9 & 8 & 2 & 1\end{array}\)
no pupils who failed the test = 1 + 3 + 4 + 7 + 10
= 25
5 of pupils who fail = \(\frac{25}{60}\) x 100%
= 41.70%

N1000
N2000
N3000
N4000
Correct answer is B
Let the monthly expenditure on school fees be x let the monthly expenditure on housing be 2x; angle of housing and school fee in a pie chart = 360o - (120o + 90o)
= 360o - 210o = 150o
Angle of housing in a pie-chart = \(\frac{2}{3}\) x 150 = 100
\(\frac{100}{360}\) x 7200 = N2,000
\(\frac{\sqrt{3}}{2}\)
\(\frac{3}{2}\)
3
\(\sqrt{3}\)cm
Correct answer is D
Length of chord = \(2r \times \sin(\frac{\theta}{2})\)
= \( 2 \times \sqrt{3} \times \sin(\frac{60}{2})\)
= \(2 \times \sqrt{3} \times \frac{1}{2}\)
= \(\sqrt{3}\) cm.
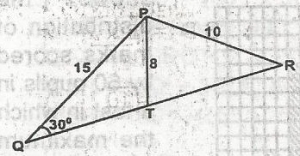
In the diagram, QTR is a straight line and < PQT = 30o. find the sin of < PTR
\(\frac{8}{15}\)
\(\frac{2}{3}\)
\(\frac{3}{4}\)
\(\frac{15}{16}\)
Correct answer is C
\(\frac{10}{\sin 30^o} = \frac{15}{\sin x} = \frac{10}{0.5} = \frac{15}{\sin x}\)
\(\frac{15}{20} = \sin x\)
sin x = \(\frac{15}{20} = \frac{3}{4}\)
N.B x = < PRQ
JAMB Subjects
Aptitude Tests