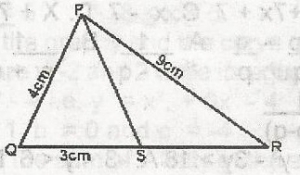
In the diagram, QPS = SPR, PR = 9cm. PQ = 4cm and QS = 3cm, find SR.
6\(\frac{3}{4}\)cm
3\(\frac{3}{8}\)cm
4\(\frac{3}{8}\)cm
2\(\frac{3}{8}\)cm
Correct answer is A
Using angle bisector theorem: line PS bisects angle QPR
QS/QP = SR/PR
3/4 = SR/9
4SR = 27
SR = \(\frac{27}{4}\)
= 6\(\frac{3}{4}\)cm
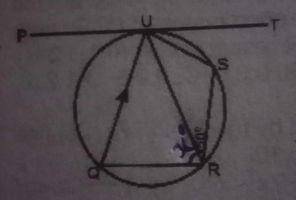
In the figure, PT is tangent to the circle at U and QU/RS if TUR = 35º and SRU = 50º find x
95o
85o
50o
35o
Correct answer is A
Since QRU= Xo
RSU = Xo, But RSU = 180o - (50o + 35o)
= 180o - 85o
= 95o
x = 95o
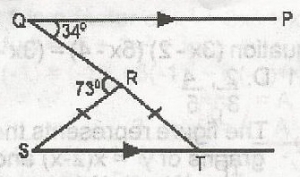
In the diagram, QP//ST:PQR = 34o qrs = 73o and Rs = RT. Find SRT
68o
102o
107o
141o
Correct answer is B
Construction joins R to P such that SRP = straight line
R = 180o - 107o
< p = 180o - (107o - 34o)
108 - 141o = 39o
Angle < S = 39o (corr. Ang.) But in \(\bigtriangleup\)SRT
< S = < T = 39o
SRT = 180 - (39o + 39o)
= 180o - 78o
= 102o

84o
48o
45o
42o
Correct answer is B
OQ = OR = radii
< ROQ = 180 - 86 = 84o
\(\bigtriangleup\)OQR = Isosceles
R = Q
R + Q + 84 = 180(angle in a \(\bigtriangleup\))
2R = 96 since R = Q
R = 48o
ORQ = 48o
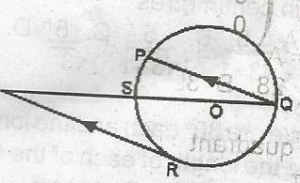
In the diagram, PQRS is a circle with O as centre and PQ/RT. If RTS = 32°. Find PSQ
32o
45o
58o
90o
Correct answer is C
< PSO = \(\frac{1}{2}\) < SOQ = \(\frac{1}{2}\)(180) = 90°
< RTS = < PQS = 32° (Alternative angle)
< PSQ = 90 - < PSQ = 90° - 32°
= 58°
JAMB Subjects
Aptitude Tests