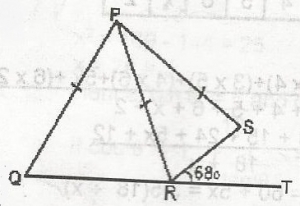
In this figure, PQ = PR = PS and SRT = 68<sup>o</sup>. Find QPS
136o
124o
12o
68o
Correct answer is A
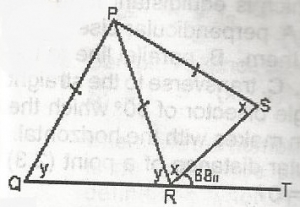
Since PQRS is quadrilateral 2y + 2x = QPS = 360o
i.e. 2(y + x) + QPS = 360o
QPS = 360o - 2(y + x)
But x + y + 68o = 180o
x + y = 180o - 68o = 180o
x + y = 180o - 68o
= 112o
QPS = 360o - 2(112o)
360o - 224o = 136o
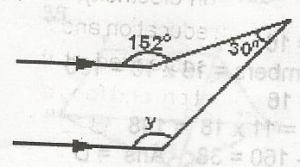
In the figure above, find the value of y
28o
122o
150o
152o
Correct answer is B
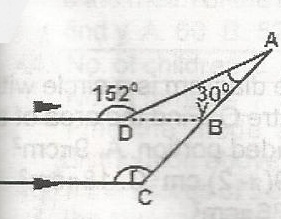
ADB = 180o - 152o = 28o
28o + y + 30o = 180o
y = 180o - 58o
= 122o
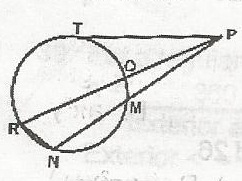
40o
30o
25o
15o
Correct answer is D
PQM = 110o(Ext. < of a cyclic quad)
MPQ = 180o - (110 + 55)
= 180o - 165o
= 15o
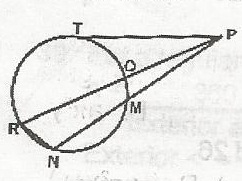
7.3, 5.9
7.7, 12.5
12.5, 7.7
5.9, 7.3
Correct answer is C
\(\frac{PQ}{PN} = \frac{PM}{PR} = \frac{QM}{NR}\)
\(\frac{4.8}{12} = \frac{5}{PR}\)
PR = \(\frac{5 \times 12}{4.8} = \frac{50}{4}\)
= 12.5
\(\frac{PQ}{PN} = \frac{PM}{PT} = \frac{TM}{NT}\)
\(\frac{PT}{12} = \frac{5}{PR}\)
PT2 = 60
PT = \(\sqrt{60}\)
= 7.746
= 7.7
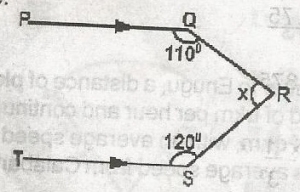
In the figure above, Find the value of x
130o
110o
100o
90o
Correct answer is A
No explanation has been provided for this answer.
JAMB Subjects
Aptitude Tests