210o
150o
105o
50o
Correct answer is D
Sum of interior angles of any polygon is (2n - 4) right angle; n angles of the nonagon = 9
where 3 are equal and 6 other angles = 1110o
( 2 x 9 - 4)90o = (18 - 4)90o
= 14 x 90o = 1260o
9 angles = 12600, 6 angles = 1110o
Remaining 3 angles = 1260o - 1110o = 150o
size of one of the3 angles \(\frac{150}{3}\) = 50o
4:9
4:5
1:3
2:3
Correct answer is B
h1 = \(\frac{h_1 + h_2}{1.5}\) = \(\frac{h_1}{h_2} = 2\)
\(\frac{A_{\bigtriangleup PQR}}{A_{TP(QRST)}} = \frac{\frac{1}{2} \times 2 \times h_1}{\frac{1}{2} \times h_2 (2 + 3)}\)
\(\frac{2}{5} \times \frac{h_1}{h_2} = \frac{2}{5} \times 2\)
= \(\frac{4}{5}\)
30o
40o
45o
50o
Correct answer is A
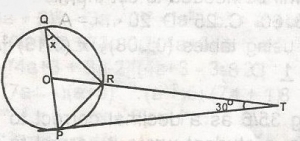
From the diagram, POQ is a diameter; o is the centre of the circle and TP is a tangent where RTP = 30o
RTP = RQP = x(at circumference = made by tangent outside the circle) i.e x = 30o
An (\(n - 2)^2\) sided figure has n diagonals. Find the number n diagonals for a 25-sided figure
7
8
9
10
Correct answer is A
(n-2)\(^2\)=25
n - 2 = 5
n = 5 + 2 = 7
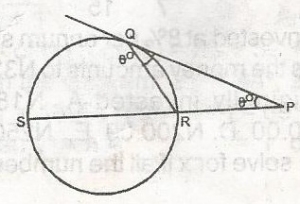
\(\theta\)o + \(\phi\)o = 902
\(\phi\)o = 902 - 2\(\theta\)o
\(\theta\)o = \(\phi\)o
\(\phi\)o = 2\(\theta\)o
\(\theta\)o + 2\(\phi\)o
Correct answer is E
180 - \(\phi\)o = \(\theta\)o + \(\phi\)o (Sum of opposite interior angle equal to its exterior angle)
180 = 2\(\phi\) + \(\theta\)o
JAMB Subjects
Aptitude Tests