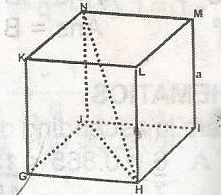
In the figure, GHIJKLMN is a cube of side a. Find the length of HN.
\(\sqrt{3a}\)
3a
3a2
a\(\sqrt{2}\)
a\(\sqrt{3}\)
Correct answer is E
HJ2 = a2 + a2 = 2a2
HJ = \(\sqrt{2a^2} = a \sqrt{2}\)
HN2 = a2 + (a\(\sqrt{2}\))2 = a2 + 2a2 = 3a2
HN = \(\sqrt{3a^2}\)
= a\(\sqrt{3}\)cm
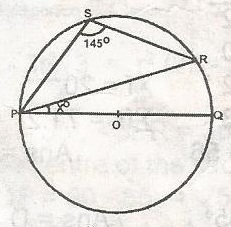
In the figure POQ is the diameter of the circle PQR. If PSR = 145o, find xo
25o
35o
45o
125o
55o
Correct answer is E
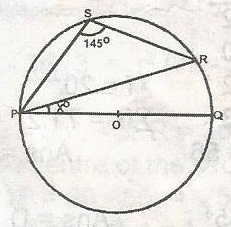
< PRQ = \(\frac{1}{2}\) < POQ = 90o
< PSR + < PQR = 180o
< PQR = 180o - 145o = 35o
\(\bigtriangleup\)PQR is a right angled triangle
x = 90 - < PQR
= 90o - 35o
= 55o
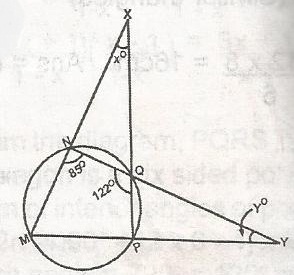
28o, 36o
36o, 28o
43o, 61o
61o, 43o
36o, 43o
Correct answer is A
yo = 180o - (86o + 58o)
180 - 144 = 36o
xo = 180 - (94 + 58)
180 -152 = 28
(xo, yo) = (28o, 36o)
190 sq.cm
20 sq.cm
210 sq.cm
160sq.cm
320sq.cm
Correct answer is C
By Pythagoras, KZ2 = 252 - 52
KZ2 = (25 + 15)(25 - 15) = 400
KZ = \(\sqrt{400}\) = 20
area of XYZ = \(\frac{1}{2} \times 28 \times 15\)
= 210 sq. cm

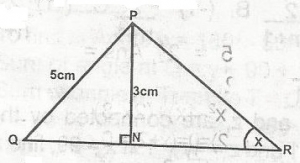
XYZ is a triangle and XW is perpendicular to YZ at = W. If XZ = 5cm and WZ = 4cm, Calculate XY.
5\(\sqrt{3}\)cm
3\(\sqrt{5}\)cm
3\(\sqrt{3}\)cm
5cm
6cm
Correct answer is B
by Pythagoras theorem, XW = 3cm
Also by Pythagoras theorem, XY2 = 62 + 32
XY2 = 36 + 9 = 45
XY = \(\sqrt{45} = 3 \sqrt{3}\)
JAMB Subjects
Aptitude Tests