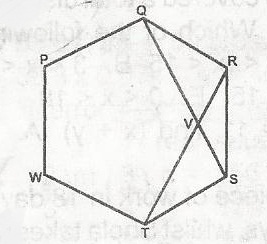
In the figure, PQRSTW is a regular hexagon. QS intersects RT at V. Calculate TVS
60o
90o
120o
30o
80o
Correct answer is A
From the diagram, PQRSTW is a regular hexagon.
Hexagon is a six sided polygon.
Sum of interior angles of polygon = (2n - 4)90o = [2 x 6 - 4] x 90 = 8 x 90 = 720o
each angle = \(\frac{720^o}{6} = 120^o\) and TVS = \(\frac{120}{2} = 60^o\)
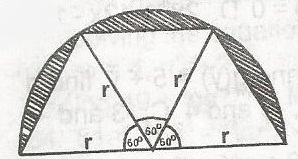
Find the area of the shaded portion of the semicircular figure.
\(\frac{r^2}{4}(4 \pi - 3 \sqrt{3})\)
\(\frac{r^2}{4}(2 \pi - 3 \sqrt{3})\)
\(\frac{1}{2}r^2 \pi\)
\(\frac{1}{8}r^2 \sqrt{3}\)
\(\frac{r^2}{4}(4 \pi - 3 \sqrt{3})\)
Correct answer is B
Asector = \(\frac{60}{360} \times \pi r^2\)
= \(\frac{1}{6} \pi r^2\)
A\(\bigtriangleup\) = \(\frac{1}{2}r^2 \sin 60^o\)
\(\frac{1}{2} r^2 \times \frac{\sqrt{3}}{2} = \frac{r^2\sqrt{3}}{4}\)
A\(\text{shaded portion}\) = Asector -
A\(\bigtriangleup\)
= (\(\frac{1}{6} \pi r^2 - \frac{r^2\sqrt{3}}{4})^3\)
= \(\frac{\pi r^2}{2} - \frac{3r^2\sqrt{3}}{4}\)
= \(\frac{r^2}{4}(2 \pi - 3 \sqrt{3})\)
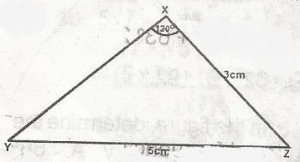
Using \(\bigtriangleup\)XYZ in the figure, find XYZ
29o
31o
31o 20'
31o 18'
Correct answer is C
\(\frac{\sin y}{3} = \frac{\sin 120^o}{5}\)
sin 120o = sin 60o
5 sin y = 3 sin 60o
sin y = \(\frac{3 \sin 60^o}{5}\)
\(\frac{3 \times 0.866}{5}\)
= \(\frac{2.598}{5}\)
y = sin-1 0.5196 = 30o 18'
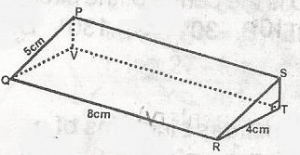
What is the volume of this regular three dimensional figure?
160cm2
48cm2
120cm2
40cm2
Correct answer is B
Volume of the three dimensional figures = v = A x h
A = \(\frac{1}{2}\) x 4 x 3
= 6cm2
V = 6 x 8
= 48cm2
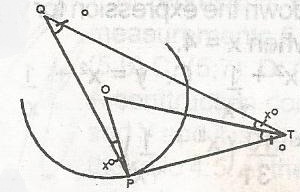
In the figure PT is a tangent to the circle with centre at O. If PQT = 30o, find the value of PTO
30o
50o
24o
12o
60o
Correct answer is B
FROM the diagram, PQT = 50o
PTQ = 50o(opposite angles are supplementary)
JAMB Subjects
Aptitude Tests