Solve \(\frac{1}{x + 1}\) - \(\frac{1}{x + 3}\) = \(\frac{1}{4}\)
x = -1 or 3
x = 1 or 3
x = 1 or -5
x = -1 or 5
x = -1 or -3
Correct answer is C
\(\frac{1}{x + 1}\) - \(\frac{1}{x + 3}\) = \(\frac{1}{4}\)
\(\frac{x + 3 - x - 1}{(x + 1)(x + 3)}\) = \(\frac{1}{4}\)
\(\frac{2}{x^2 + 4x + 3}\) = \(\frac{1}{4}\)
= x2 + 4x + 3 = 8
x2 + 4x - 5 = 0
= (x - 1)(x + 5) = 0
x = 1 or -5
Simplify \(\frac{\sqrt{2}}{\sqrt{3} - \sqrt{2}}\) - \(\frac{3 - 2}{\sqrt{3} + \sqrt{2}}\)
2\(\sqrt{2} - \sqrt{3}\)
3(\(\sqrt{6}\) - 1)
\(\sqrt{6}\) - 3
-\(\frac{1}{2}\)
\(\frac{-\sqrt{3}}{\sqrt{2} - \sqrt{2}}\)
Correct answer is B
\(\frac{\sqrt{2}}{\sqrt{3} - \sqrt{2}}\) - \(\frac{3 - 2}{\sqrt{3} + \sqrt{2}}\)
\(\frac{\sqrt{2}}{\sqrt{3} - \sqrt{2}}\) = \(\frac{\sqrt{2}}{\sqrt{3}}\) - \(\frac{x}{\sqrt{2}}\)
\(\frac{\sqrt{3} + \sqrt{2}}{3 + \sqrt{2}}\) = \(\sqrt{6}\) + 2
\(\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}\) = \(\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}\) x \(\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}}\)
= 5 - 2\(\sqrt{6}\)
\(\sqrt{6}\) + 2 - (5 - 2 \(\sqrt{6}\)) = \(\sqrt{6}\) + 2 - 5 + 2\(\sqrt{6}\)
= 3\(\sqrt{6}\) - 3
= 3(\(\sqrt{6}\) - 1)
In one and a half hours, the minute hand of a clock rotates through an angle of
90o
180o
640o
450o
540o
Correct answer is E
1 hr = 60 mins, 60 mins = 360°
30 mins = \(\frac{360^o}{1}\) × \(\frac{30}{60}\)
= 180°
90 mins = 360° + 180°
= 540°
0.00012m
0.0000012m
0.000012m
0.00000012m
0.000000012m
Correct answer is C
1 UM = 10-6mm = 10-9m
1.2 x 104 x 10-9m = 1.2 x 10-5m (0.000012)
7cm
12cm
8cm
36cm
69cm
Correct answer is A
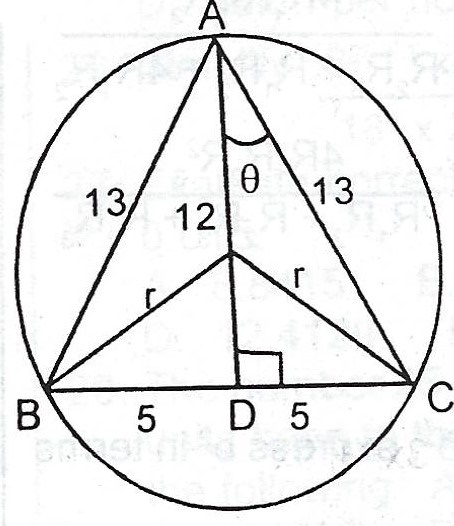
In \(\Delta DAC, \stackrel\frown{DAC} = \theta\)
\(\sin \theta = \frac{5}{13}\)
\(\theta = 22.6°\)
\(< DOC = 22.6° \times 2 = 45.2°\)
\(\sin 45.2 = \frac{5}{r} \implies r = \frac{5}{\sin 45.2}\)
\(r = 7.046cm\)
= \(7\frac{1}{24} cm\)
JAMB Subjects
Aptitude Tests