Given that r = \( \sqrt \frac{3v}{\pi h} \), make v the subject of the formula
v = 3 \(πr^2\) h
v = \(\frac{πrh}{3}\)
v = \(\frac{πr^2h}{3}\)
v = 3πrh
Correct answer is C
square both sides to remove the big square root
→ r\(^2\) = \(\frac{3v}{πh}\)
cross multiply
3v = r\(^2\) * πh
v = \(\frac{πr^2h}{3}\)
\(\begin{pmatrix} 18 & 6 \\ 12 & 10 \\ 10 & 6 \end{pmatrix}\)
\(\begin{pmatrix} 10 & 6 \\ 13 & 10 \\ 12 & 6 \end{pmatrix}\)
\(\begin{pmatrix} 10 & 6 \\ 12 & 10 \\ 11 & 6 \end{pmatrix}\)
\(\begin{pmatrix} 10 & 6 \\ 18 & 10 \\ 11 & 6 \end{pmatrix}\)
Correct answer is D
Given A = \(\begin{pmatrix} 2 & 1 \\ 2 & 3 \\ 1 & 2 \end{pmatrix}\) and B = \(\begin{pmatrix} 3 & 2 \\ 4 & 2 \end{pmatrix}\).
We can multiply these matrices since the number of colums in A = number of rows in B
AB = \(\begin{pmatrix} (2*3)+(1*4) & (2*2)+(1*2) \\ (2*3)+(3*4) & (2*2)+(3*2) \\ (1*3)+(2*4) & (1*2)+(2*2) \end{pmatrix}\)
AB = \(\begin{pmatrix} (6+4) & (4+2) \\ (6+12) & (4+6) \\ (3+8) & (2+4) \end{pmatrix}\)
= \(\begin{pmatrix} 10 & 6 \\ 18 & 10 \\ 11 & 6 \end{pmatrix}\)
\(\frac{{2x+1}^3}{8}\) + C
\(\frac{{2x+1}^4}{8}\) + C
\(\frac{{2x+1}^4}{4}\) + C
\(\frac{{2x+1}^2}{6}\) + C
Correct answer is B
Recall chain rule:
u = 2x +1; du = 2dx → dx = \(\frac{du}{2}\)
u\(^3\) = ∫ u\(^3\) \(\frac{du}{2}\) → \(\frac{1}{2}\) ∫ u\(^3\)
= \(\frac{1*u^4}{2*4}\)
= \(\frac{u^4}{8}\) → \(\frac{{2x+1}^4}{8}\) + C
In how many ways can the letter of ZOOLOGY be arranged?
720
360
840
120
Correct answer is C
Zoology has 7 letters in total, with O repeated thrice
\(\frac{7!}{3!}\) → \(\frac{7*6*5*4*3*2*1}{3*2*1}\)
= 840ways
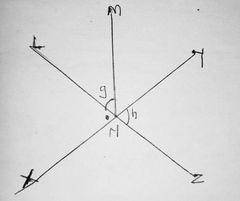
In the diagram above angle LNM and angle YNZ are represented by g and h respectively. Find ∠MNY
180º - gº - hº
360º - (g-h)º
180º - (g-h)º
360º - gº - hº
Correct answer is A
Using line LZ with angles sum = 180º
: ∠MNY = 180º - (g + h)º or 180º - gº - hº
JAMB Subjects
Aptitude Tests