9.0 m
12. 0 m
8.8 m
10.4 m
Correct answer is B
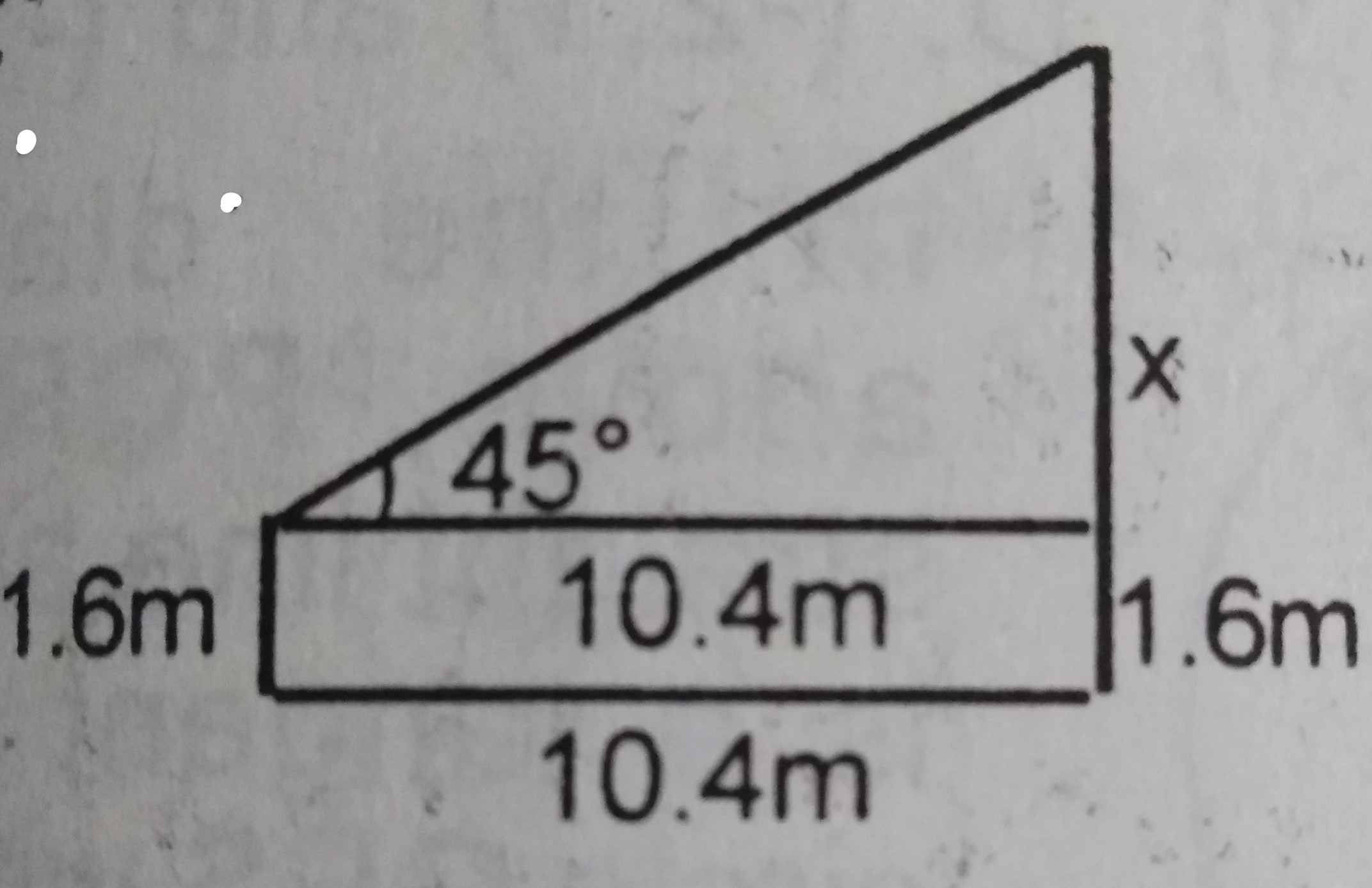
\(\tan 45 = \frac{x}{10.4}\) = 10.4m
\(height of the tree is equal to 1.6m + 10.4m=12m\)
Find the coordinates of the mid-point of x and y intercepts of the line 2y = 4x - 8
(2, 0)
(1, -2)
(-1, -2)
(1, 2)
Correct answer is B
2y = 4x - 8 \(\implies\) y = 2x - 4.
When x = 0, y = -4.
When y = 0, x = 2.
The midpoint between (0, -4) and (2, 0) = \((\frac{0 + 2}{2}, \frac{-4 + 0}{2})\)
= \((1, -2)\)
12
20
40
10
Correct answer is A
The formula for the sum of the interior angles of a regular polygon = (2n - 4) x 90°
Given: Sum = 20 right angles
(2n - 4) x 90° = 20 \times 90°
⇒ 2n - 4 = 20
2n = 24; n = 12.
304π/3 cm3
144π cm3
128π cm3
72π cm3
Correct answer is A
Volume of a frustrum with top of radius R and bottom r and height h = \(\frac{1}{3} \pi (R^{2} + Rr + r^{2})\)
V = \(\frac{1}{3} \pi \times 4 \times (6^2 + 6 \times 4 + 4^2)\)
= \(\frac{304}{3} \pi cm^{3}\)
Find the equation of the set of points which are equidistant from the parallel lines x = 1 and x = 7
y = 3
x = 3
x = 4
y = 4
Correct answer is C
The line equidistant from x = 1 and x = 7 is
\(x = \frac{1 + 7}{2} \implies x = 4\)
JAMB Subjects
Aptitude Tests