JAMB Physics Past Questions & Answers - Page 438

2,186.

The diagram above shows two capacitors P and Q of capacitance 5μF and 10μF. Find the charges stored in P and Q respectively

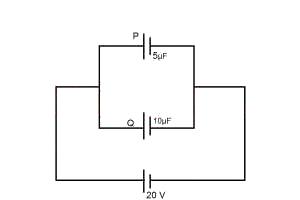
2μC and 4μC

4μC and 2μC

100μC and 200μC

200μC and 100μC

View answer & explanation

Correct answer is C

Since capacitance C = Q/V, => Q = CV
∴ Qp = 5 x 10-b x 20
= 100 x 10-b or 100μC
Qp = 10 x 10-b x 70
= 200 x 10-b or 200μC
Correct option 100μC and 200μC

2,187.

A transverse wave is applied to a string whose mass per unit length is 3 x 10-2kgm-1. If the string is under a tension 12N, the speed of the propagation of the wave is

5 ms^-1

20 ms^-1

30 ms^-1

40 ms^-1

View answer & explanation

Correct answer is B

For transverse wave on string
velocity V = √T/M
where T is the tension, and M is the mass per unit length
∴ for T = 12N and M = 3.0 x 10-2kgm-1
V=
√ 12 / (3.0x10-2

=
√ 12 / 0.03

=
√ 1200 / 3

=
√ 1200 / 3 = 20

∴V = 20m/s

2,188.

A travelling wave moving from left to right has an amplitude of 0.15m, a frequency of 550Hz and a wavelength of 0.01m. The equation describing the wave is

y = 0.15 sin 200π(x - 5.5t)

y = 0.15 sin π(0.01x - 5.5t)

y = 0.15 sin 5.5π(x - 200t)

y = 0.15 sin π(550x - 0.01t)

View answer & explanation

Correct answer is A

The general wave equation is given by Y = sin A ^2π/_λ [x - vt]
= Sin A [(2π X)/λ - (2π vt)/λ]
thus if A = 0.15;λ = 0.01m; f = 550Hz
then V = f x λ = 550 x 0.01 = 5.50m/s
∴ Y = 0.15 sin [(2 x λ x X)/0.01 - (2 x λ x 5.5t)/0.01]
= 0.15 sin[200λX - 200 x λ x 5.5t]
∴ Y = 0.15 sin 200λ[x - 5.5t]

2,189.

A sonometer wire is vibrating at frequency f_o. If the tension in the wire is doubled while the length and the mass per unit length are kept constant, the new frequency of vibration is

^f_o/₂

2f_o

^f_o/_√2

f_o√2

View answer & explanation

Correct answer is D

For a vibrating sonometer wire, the frequency
F = l/2l √(T/m)
and if the length, l and mass per unit length, m, are constant, then Fo ∝ √T => FoK√T or Fo/√T = K
=> F1o/√F1 = F2o/√F2
∴ F1o/√T1 = F2o/√T2

thus F2 =	F3x√(2T1
	__√T1

=	Fox√2 x √T1
	√T1

∴F2 = Fo x √2 = Fox√2

2,190.

A simple pendulum has a period of 17.0s. When the length is shorten by 1.5m, its period is 8.5s. Calculate the original length of the pendulum

4.0 m

5.0 m

2.0 m

1.5 m

View answer & explanation

Correct answer is C

For a simple pendulum, the period T = 2π
√ ¹/_g

Since g, 2 and π are constant, => T ∝ √l
∴ T = K√l
Let the original length = l
thus for the length l, period T = 17s
∴ 17 = K√1 .................. [1]
Again, for the new length [1 - 1.5]
the period T = 8.5s
∴ 8.5 = k
√ [1-1.5] ...............[2]

thus dividing eqn [1] by eqn[2] we have
¹⁷/_8.5 = √(l/l-1.5)
∴2 = √(l/l-1.5)
=>4 = (l/l-1.5)
∴l = 4[l-1.5]
= 4l - 6.0
∴4l - l = 6.0
3l = 6.0
l = 2.0m