6
25
15
18
Correct answer is C
\(m \otimes n = mn + m - n\)
3 \(\otimes\) (2 \(\otimes\) 4)
2 \(\otimes\) 4 = 2(4) + 2 - 4 = 6
3 \(otimes\) 6 = 3(6) + 3 - 6 = 15
148m
382m
282m
248m
Correct answer is C
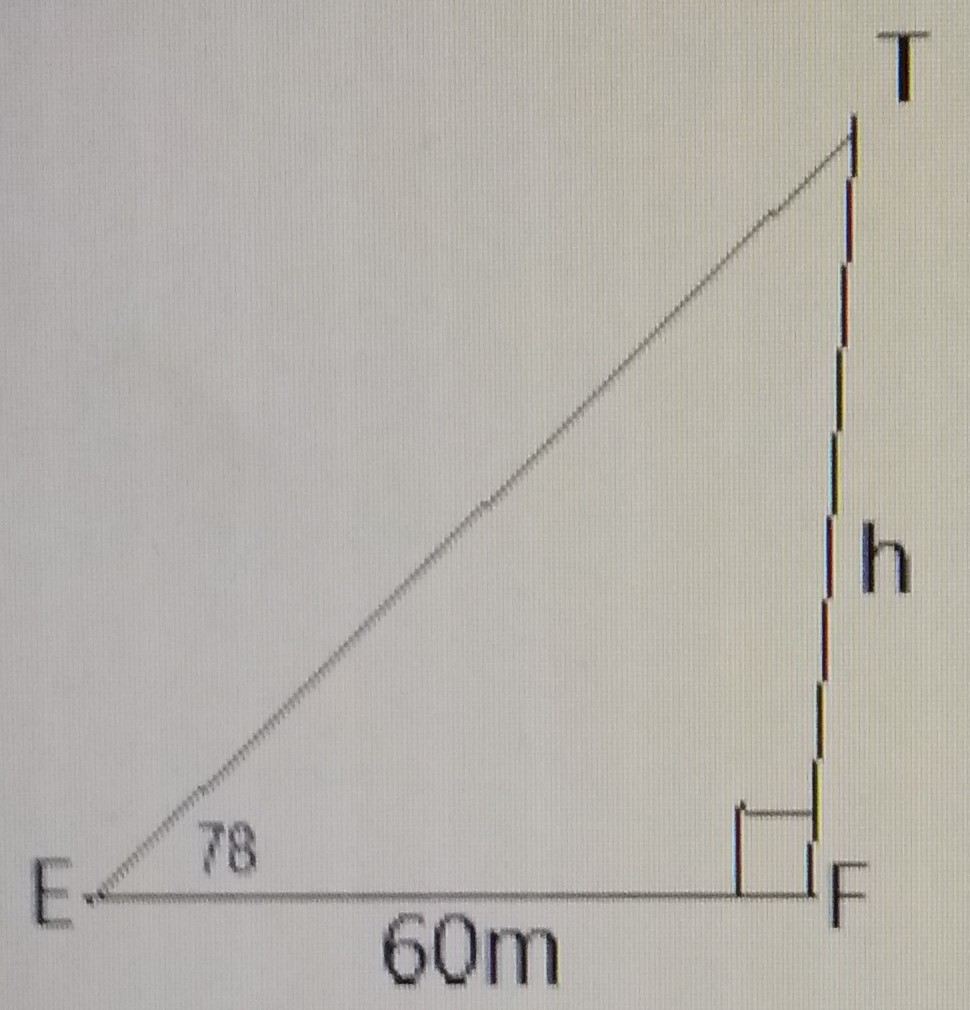
\(\tan 78 = \frac{h}{60}\)
\(h = 60 \tan 78\)
\(h = 60 \times 4.705 = 282.27m\)
\(\approxeq\) 282m to the nearest whole number.
Make q the subject of the formula in the equation \(\frac{mn}{a^2} - \frac{pq}{b^2} = 1\)
\(q = \frac{b^2(mn - a^2)}{a^2 p}\)
\(q = \frac{m^2 n - a^2}{p^2}\)
\(q = \frac{mn - 2b^2}{a^2}\)
\(q = \frac{b^2 (n^2 - ma^2)}{n}\)
Correct answer is A
\(\frac{mn}{a^2} - \frac{pq}{b^2} = 1\)
\(\frac{mn}{a^2} - 1 = \frac{pq}{b^2}\)
\(\frac{mn - a^2}{a^2} = \frac{pq}{b^2}\)
\(pq = \frac{b^2 (mn - a^2)}{a^2}\)
\(q = \frac{b^2(mn - a^2)}{a^2 p}\)
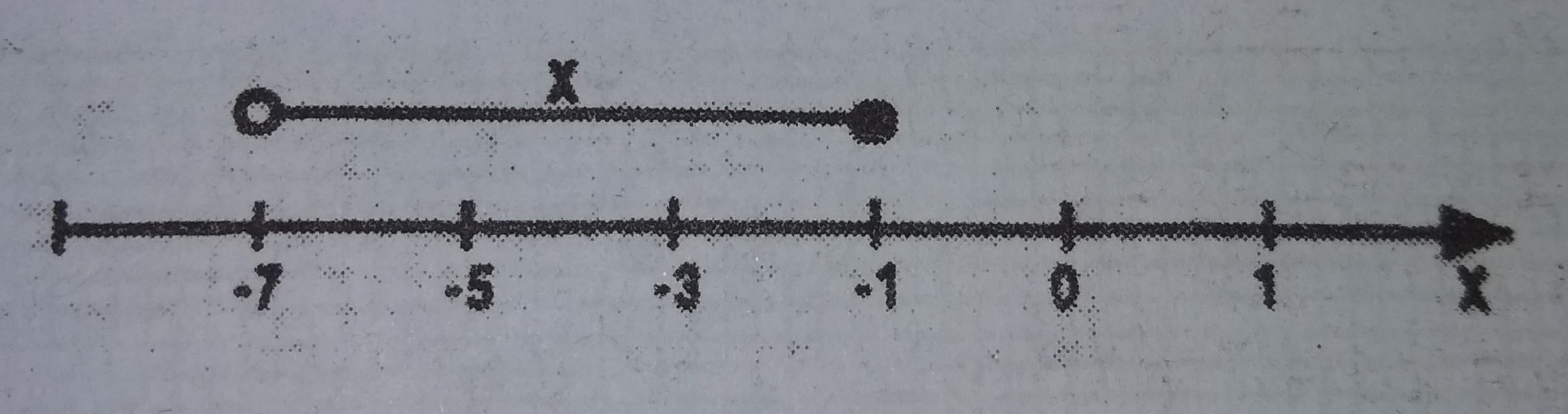
0 > x \(\geq\) -7
-7 \(\leq\) x < -1
-7 < x \(\leq\) -1
-7 < x < -1
Correct answer is C
No explanation has been provided for this answer.
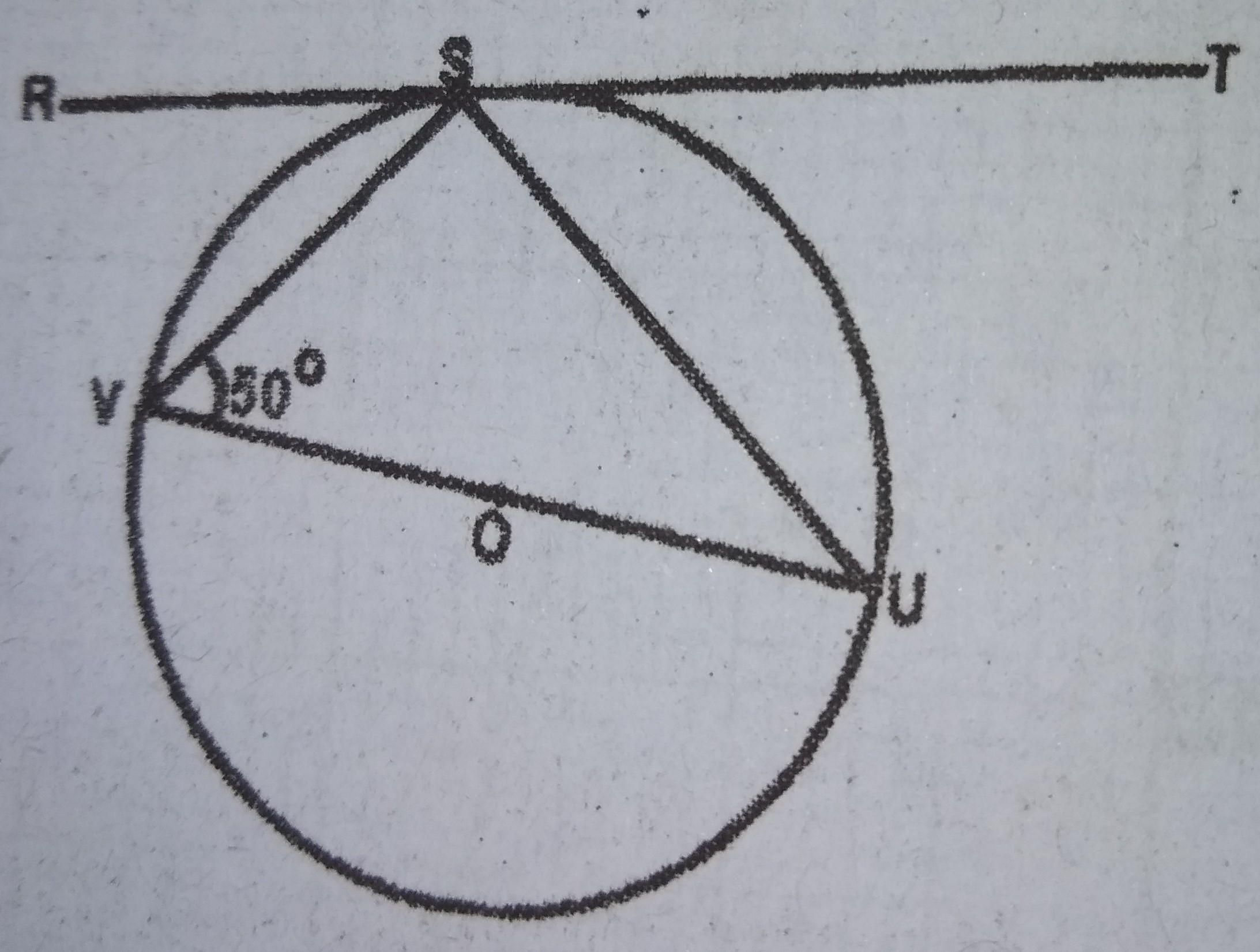
90°
50°
45°
40°
Correct answer is D
< VSU = 90° (angle in a semi-circle)
\(\therefore\) < SUV = 180° - 90° - 50°
= 40°
< RSV = 40° (angle which chord makes tangent = angle in alternate segment)
JAMB Subjects
Aptitude Tests