Calculate the area of an equilateral triangle of side 8cm
8√3
16
4√3
16√3
Correct answer is D
An equilateral triangle has all sides equal and all angles equal as 600
Area = \(\frac{1}{2}\) absinθ
Area = \(\frac{1}{2}\) x 8 x 8 x sin60
= \(\frac{1}{2}\) x 64 x \(\sqrt{\frac{3}{2}}\)
= 16√3 cm\(^2\)
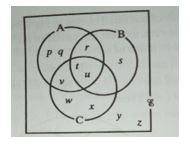
Which one of the following gives the members of the set A1 n B n C?
Φ
{s}
{t, u}
{y, z}
Correct answer is A
A1 = Elements in the universal set but not in A = {s, w, x, y, z} B = {r, s. t, u} C = {t, u, v, w, x} A1 n B n C = elements common to the three sets = none = empty set = Φ
\(\frac{2}{3}\)
\(\frac{1}{3}\)
\(\frac{1}{4}\)
\(\frac{1}{9}\)
Correct answer is D
Total number of balls = 2 + 4 = 6
P(of picking a red ball) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
P(of picking a blue ball) = \(\frac{4}{6}\) = \(\frac{2}{3}\)
With replacement,
P( picking two red balls) = \(\frac{1}{3}\) × \(\frac{1}{3}\) = \(\frac{1}{9}\)
if y = 23\(_{five}\) + 101\(_{three}\) find y leaving your answer in base two
1110
10111
11101
111100
Correct answer is B

First we convert the numbers to base ten
23\(_{five}\)= 2 x 51 + 3 x 50
= 10 + 3 = 13
101\(_{five}\) = (1 x 32) + (0 x 31) + (1 x 30)
= 9 + 0 + 1 = 10
So, y = 13 + 10 = 23
To convert 23 to base 2 (as in the diagram above)
Y = 23
= 10111\(_{five}\)
Answer is B
From a point P, Q is 5km due West and R is12km due South of Q. Find the distance between P and R.
5km
12km
13km
17km
Correct answer is C
Using Pythagoras theorem
PR\(^2\) = 5\(^2\) + 12\(^2\)
25 + 144 = 169
PR = √(169)= 13km
JAMB Subjects
Aptitude Tests