Tanθ is positive and Sinθ is negative. In which quadrant does θ lies
Second only
Third only
Fourth only
First and third only
Correct answer is B
First quadrant: Sin, Cos and Tan are all positive Second quadrant: Sin is positive, Cos is negative and Tan is negative Third quadrant: Tan is positive, Sin is negative and Cos is negative Fourth quadrant: Cos is positive, Sin is negative and Tan is negative The correct option is the third quadrant only where Tanθ is positive and Sinθ is negative
Evaluate log\(_2\) 8 – log\(_3\) \(\frac{1}{9}\)
-1 1\(\frac{1}{2}\)
-1
1
5
Correct answer is D
log\(_2\) 8 – log\(_3\) \(\frac{1}{9}\)
= log \(_2\) 2\(^3\) – log\(_3\) 9\(^{-1}\)
= log\(_2\) 2\(^3\) – log\(_3\) 3\(^{-2}\)
Based on law of logarithm
= 3 log\(_2\) 2 – (-2 log\(_3\) 3)
But log\(_2\) 2 = 1,
log\(_3\) 3 = 1
So, = 3 + 2
= 5
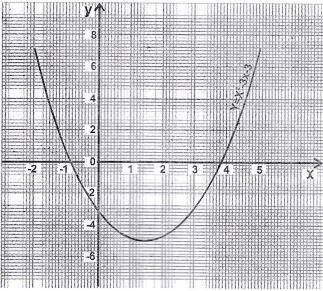
Use the quadratic equation curve to answer this questions
What is the minimum value of the graph?
-5.3
0.5
3
8
Correct answer is A
The minimum value is the lowest value of the curve on y axis which gives a value of -5.3
Find the equation of the tangent at the point (2, 0) to the curve y = x\(^2\) - 2x
y = 2x - 4
y = 2x + 4
y = 2x - 2
y = 2x + 2
Correct answer is A
The gradient to the curve is found by differentiating the curve equation with respect to x
So \(\frac{dy}{dx}\) 2x - 2
The gradient of the curve is the same with that of the tangent.
At point (2, 0) \(\frac{dy}{dx}\) = 2(2) - 2
= 4 – 2 = 2
The equation of the tangent is given by (y - y1) \(\frac{dy}{dx}\) (x – x1)
At point (x1, y1) = (2, 0)
y - 0 = 2(x - 2)
y = 2x - 4
-4
-2
2
4
Correct answer is A
2√3 - 4) ( 2√3 + 4) = 12 + 8√3 - 8√3 – 16 = 12 – 16 = -4 The two expressions in the bracket are conjugate of each other
JAMB Subjects
Aptitude Tests