| Mark | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 2 | 7 | 5 | 4 | 3 |
What is the probability of selecting a student from the group that scored 2 or 3
\(\frac{1}{11}\)
\(\frac{5}{22}\)
\(\frac{7}{22}\)
\(\frac{6}{11}\)
Correct answer is D
No explanation has been provided for this answer.
| Mark | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 2 | 7 | 5 | 4 | 3 |
What is the median mark?
1
2
3
4
Correct answer is C
Total frequency = 1 + 2 + 7 + 5 + 4 + 3 = 22
Median is the middle number
= \(\frac{Nth}{2}\)
term = \(\frac{22th}{2}\) = 11th term
Going in ascending order, 11th term is 3, going in descending order 11th term is 3
Median = 3 + \(\frac{3}{2}\) = \(\frac{6}{2}\) = 3
Answer is C
N676.50
N820
N1,640
N4,920
Correct answer is C
No explanation has been provided for this answer.
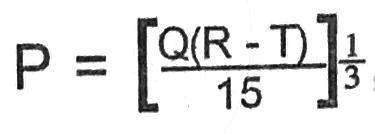
Make T the subject of the relation.
T = \(\frac{R + P3}{15Q}\)
T = \(\frac{R - 15P^3}{Q}\)
T =R - \(\frac{15P^3}{Q}\)
T = \(\frac{15R + Q}{P^3}\)
Correct answer is C
P = (\(\frac{Q( R - T )}{ 15})^\frac{1}{3}\)
take cube of both sides
\(P^3 =\frac{Q( R - T)}{ 15}\)
cross multiply
\(15P^3 = Q( R - T)\)
\(\frac{15P^3}{Q}\) = R - T
T = R - \(\frac{15P^3}{Q}\)
25
1
\(\frac{1}{5}\)
\(\frac{1}{25}\)
Correct answer is A
\(\frac {25^{\frac{2}{3}} \div 25^{\frac{1}{6}}} {(\frac{1}{5})^{\frac{7}{6}} \div (\frac{1}{5})^{\frac{1}{6}}}\)
= \(\frac{25^{\frac{2}{3} - \frac{1}{6}}}{(\frac{1}{5})^{\frac{7}{6} - \frac{1}{6}}}\)
= \(\frac{25^{\frac{1}{2}}}{(\frac{1}{5})}\)
= \(5 \div \frac{1}{5}\)
= 25
JAMB Subjects
Aptitude Tests