Solve for t in the equation \(\frac{3}{4}\)t + \(\frac{1}{3}\)(21 - t) = 11
\(\frac{9}{13}\)
\(\frac{7}{13}\)
5
9\(\frac{3}{5}\)
Correct answer is D
\(\frac{3}{4}\) t + \(\frac{1}{3}\) (21 - t) = 11
Multiply through by the LCM of 4 and 3 which is 12
12 x(\(\frac{3}{4}\) t) + 12 x (\(\frac{1}{3}\) (21 - t)) = (11 x 12)
9t + 4(21 - t) = 132
9t + 84 - 4t = 132
5t + 84 = 132
5t = 132 - 84 = 48
t = \(\frac{48}{5}\)
t = 9 \(\frac{3}{5}\)
Answer is D
If y = 23\(_{five}\) + 101\(_{three}\) , find y, leaving your answer in base two
1110
10111
11101
111100
Correct answer is B
y = 23\(_{five}\) + 101\(_{three}\)
23\(_{five}\) = \(2 \times 5^1 + 3 \times 5^0\)
= 13\(_{ten}\)
101\(_{three}\) = \(1 \times 3^2 + 0 \times 3^1 + 1 \times 3^0\)
= 10\(_{ten}\)
y\(_{ten}\) = 13\(_{ten}\) + 10\(_{ten}\)
= 23\(_{ten}\)
= 10111\(_{two}\)
7
6
5
4
Correct answer is C
Profit (P) = 10\(_x\) − \(_x\)2
Maximum profit can be achieved when the differential of profit with respect to number of bags(x) is 0
i.e. \(\frac{dp}{dx}\) = 0
\(\frac{dp}{dx}\) = 10 - 2x = 0
10 = 2x
Then x = \(\frac{10}{2}\) = 5
Answer is C
1000
2000
3000
4000
Correct answer is B
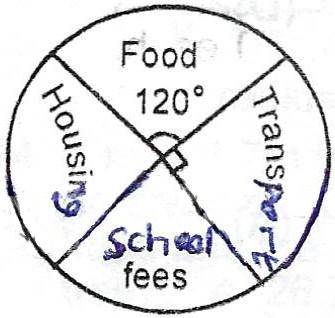
Let the angle for school fees = x°
Then Housing = 2x°
120° + 90° + x° + 2x° = 360°
3x° = 150° \(\implies\) x° = 50°.
Amount spent on housing = \(\frac{100}{360} \times 7200\)
= N2000.
Find the values of x for which \(\frac {x+2}{4}\) - \(\frac{2x - 3}{3}\) < 4
x < 8
x > -6
x < 4
x > -3
Correct answer is B
\(\frac {x+2}{4}\) - \(\frac{2x - 3}{3} < 4\)
\(\frac{3(x + 2) - 4(2x - 3)}{12} < 4\)
\(3x + 6 - 8x + 12 < 48 \)
\(18 - 5x < 48 \implies -5x < 30\)
\(\therefore x > -6\)
JAMB Subjects
Aptitude Tests