1360cm\(^3\)
600cm\(^3\)
240cm\(^3\)
8000m\(^3\)
Correct answer is B
\(Density= \frac{mass}{volume}\)
⇒ \(0.9gcm^{-3} = \frac{mass}{400cm^{3}} = 360g\)
without any loss in the frying process, we have
\(0.6gcm^{-3} = \frac{360g}{v}\)
\(v = \frac{360g}{0.6gcm^{-3}} = 600cm^{3}\)
A man walks 1km due east and then 1 km due north His displacement?
√2km N 45°E
1km N 30°E
1km N 15°E
√2km N 60°E
Correct answer is A
His movements 1km due east and then 1 km due north make a Right-Angled Triangle.
Using Pythagoras' theorem;
The Resultant becomes the Hypotenuse [h]
Hyp\(^2\) = Adj\(^2\) + \Opp(^2\)
Hyp\(^2\) = 1\(^2\) + 1\(^2\)
Hyp\(^2\) = 2 → Hyp = √2
: Resultant = √2
DIRECTION TAN Ø = \(\frac{OPP}{ADJ}\)
TAN Ø = \(\frac{1}{1}\)
Ø = TAN\(^{-1}\) [1]
Ø= 45°
Displacement is √2km N 45°E
Which of the following representations is correct for an atom X with 28 electrons and 30 neutrons?
\(^{58}_{28}X\)
\(^{30}_{28}X\)
\(^{28}_{30}X\)
\(^{58}_{30}X\)
Correct answer is A
An atom can be represented thus,
\(^{Z}_{A}X\) where Z = mass number
A = atomic number
A = number of proton = number of electrons in a free state = 28
Z = number of protons + number of neutrons = 28 + 30 = 58
\(^{58}_{28}X\)is the representation
30cm3
40cm3
50cm3
20cm3
Correct answer is D
Using boyle's law
P1V1 = P2V2
V2 = \(\frac{P_1 V_1}{200}\) = \(\frac{400 \times 10}{200}\)
= 20cm3
The velocity ratio of an inclined plane where angle of inclination in θ is
Sinθ
Cosθ
Tanθ
\(\frac{1}{\sin \theta}\)
Correct answer is D
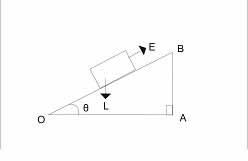
Consider an inclined plane shown below, as the effort moves along OB, the load moves is lifted up through a vertical height AB
V.R = \(\frac{\text{distance moved by effort}}{\text{distance moved by load}}\) = \(\frac{OB}{AB}\)
But Sinθ = \(\frac{opp}{hyp}\) = \(\frac{AB}{OB}\)
therefore; = \(\frac{OB}{AB}\) = \(\frac{1}{\sin \theta}\)
JAMB Subjects
Aptitude Tests