Rationalize \(\frac{\sqrt{6} - \sqrt{4}}{\sqrt{6} + \sqrt{4}}\)
5 + 2 \(\sqrt{6}\)
5 - 4 \(\sqrt{6}\)
5 + 4 \(\sqrt{6}\)
5 - 2 \(\sqrt{6}\)
Correct answer is D
\(\frac{\sqrt{6} - \sqrt{4}}{\sqrt{6} + \sqrt{4}}\) = \(\frac{6-2\sqrt{6} - 2\sqrt{6} + 4}{6 - 4}\)
\(\frac{10 - 4\sqrt{6}}{2}\) = 5 - 2\(\sqrt{6}\)
Third quartile range
Semi-quartile range
Cummulative frequency table
Inter-quartile table
Correct answer is B
No explanation has been provided for this answer.
Find the mean of 10, 8, 5, 11, 12, 9, 6, 3, 15, and 23.
11.2
10
10.2
11.3
Correct answer is C
\(\frac{10 + 8 + 5 + 11 + 12 + 9 + 6 + 3 + 15 + 23}{10}\)
= \(\frac{102}{10}\) = 10.2
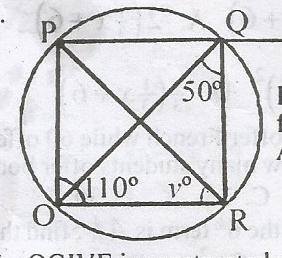
From the cyclic quadrilateral above, find < TSV
60o
80o
70o
50o
Correct answer is B
< TVS = 180o - (80 + 20)
= 180 - 100 = 80o
If Q is a factor of 18 and T is prime numbers between 2 and 18. What is Q\(\cap\)T?
(2,3)
(2,3,18)
(2,3,9)
(2,3,6)
Correct answer is A
Q = {1,2,3,6,9,18}, T = {2,3,5,7,11,13,17}
Q\(\cap\)T = {2,3}
JAMB Subjects
Aptitude Tests