
Further Mathematics Questions and Answers
Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.

Test your knowledge of advanced level mathematics with this aptitude test. This test comprises Further Maths questions and answers from past JAMB and WAEC examinations.
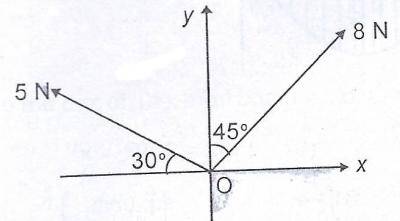
14.06N
13.00N
9.83N
8.26N
Correct answer is D
No explanation has been provided for this answer.
1.7N
4.5N
9.0N
13.0N
Correct answer is A
\(F = F \cos \theta + F \sin \theta\)
where \(F \cos \theta = \text{horizontal component}\)
\(F \sin \theta = \text{vertical component}\)
Horizontal component of resultant = sum of horizontal compoents of individual forces
= \(8 \cos 30 + 10 \cos 150 = 6.928 - 8.66 \approxeq - 1.7N\)
The sum, \(S_{n}\), of a sequence is given by \(S_{n} = 2n^{2} - 5\). Find the 6th term
112
67
45
22
Correct answer is D
\(S_{n} = 2n^{2} - 5\)
\(T_{n} = S_{n} - S_{n - 1}\)
\(T_{6} = S_{6} - S_{5}\)
= \((2(6^{2} - 5) - (2(5^{2} - 5) = 62 - 40 = 22\)
22m
18m
14m
10m
Correct answer is C
\(a = \frac{v - u}{t} = \frac{9 - 5}{2} = 2 ms^{-2}\)
\(s = ut + \frac{1}{2}at^{2} = 5(2) + \frac{1}{2}(2 \times 2^{2})\)
= \(14m\)
If \(2\sin^{2} \theta = 1 + \cos \theta, 0° \leq \theta \leq 90°\), find the value of \(\theta\).
90°
60°
45°
30°
Correct answer is B
\(2\sin^{2} \theta = 1 + \cos \theta\)
\(2 ( 1 - \cos^{2} \theta) = 1 + \cos \theta\)
\(2 - 2\cos^{2} \theta = 1 + \cos \theta\)
\(0 = 1 - 2 + \cos \theta + 2\cos^{2} \theta\)
\(2\cos^{2} \theta + \cos \theta - 1 = 0\)
Factorizing, we have
\((\cos \theta + 1)(2\cos \theta - 1) = 0\)
Note: In the range, \(0° \leq \theta \leq 90°\), all trig functions are positive, so we consider
\(2\cos \theta = 1 \implies \cos \theta = \frac{1}{2}\)
\(\theta = 60°\).