Find the area of the shades segments in the figure
...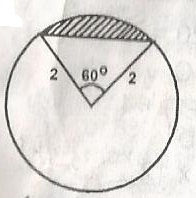
Find the area of the shades segments in the figure
\(\sqrt{3}\)
4 \(\pi - \sqrt{3}\)
-\(\frac{2}{3} \pi\)
\(\frac{2\pi}{3}\) -3
Correct answer is D
Area of section = \(\frac{60^o}{360^o}\) x 11r2
= \(\frac{60}{360} \times \pi \times 2^2\)
= \(\frac{1}{6}\) x 4
= \(\frac{4\pi}{6}\)
= \(\frac{2\pi}{3}\)
Area of triangle = \(\frac{1}{2x}\)
= 2 x 28.......60
Segment Area = Area of section - Area of triangle
= \(\frac{2\pi}{3}\) -3
Similar Questions
Simplify \(\frac{\sqrt{8^2 \times 4^{n + 1}}}{2^{2n} \times 16}\)...
In the diagram above MN is a chord of a circle KMN centre O and radius 10cm. If < MON = 140&...
Two fair dice are rolled. What is the probability that both show up the same number of points....
Which of the following numbers is perfect cube?...
Find the curved surface area of the frustrum in the figure ...
The bearing of Q from P is 122o, what is the bearing of P from Q?...
The roots of a quadratic equation in x, are -m and 2n. Fine equation. ...