In the figure, the area of the shaded segment is
...
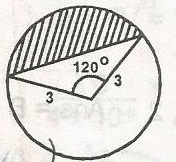
In the figure, the area of the shaded segment is
3\(\pi\)
9\(\frac{\sqrt{3}}{4}\)
3 \(\pi - 3 \frac{\sqrt{3}}{4}\)
\(\frac{(\sqrt{3 - \pi)}}{4}\)
\(\pi + \frac{9 \sqrt{3}}{4}\)
Correct answer is C
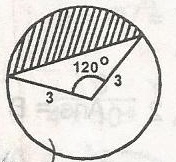
Area of sector = \(\frac{120}{360} \times \pi \times (3)^2 = 3 \pi\)
Area of triangle = \(\frac{1}{2} \times 3 \times 3 \times \sin 120^o\)
= \(\frac{9}{2} \times \frac{\sqrt{3}}{2} = \frac{9\sqrt {3}}{4}\)
Area of shaded portion = 3\(\pi - \frac{9\sqrt {3}}{4}\)
= 3 \(\pi - 3 \frac{\sqrt{3}}{4}\)
Similar Questions
A trader bought 100 oranges at 5 for N40.00 and 20 for N120.00. Find the profit or loss percent ...
The 10th term of an AP is 32. If the first term is 3/2, what is the 4th term? ...
Simplify: \(\frac{54k^2 - 6}{3k + 1}\)...
If the numbers M, N, Q are in the ratio 5:4:3, find the value of \(\frac{2N - Q}{M}\)...
If log\(_x\) 2 = 0.3, evaluate log\(_x\) 8....
Make q the subject of the relation t = √(pq/r - r\(^2\)q)...