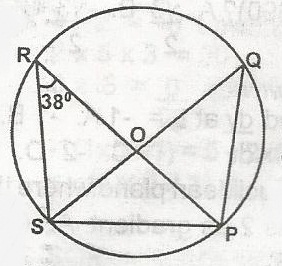
In the diagram, O is the centre of the circle. If SOQ is a diameter and < PRS is 38o, what is the value of < PSQ
148o
104o
80o
52o
Correct answer is D
< SRP = < SQP = 38o (angle in the same segment of a circle are equal)
But < SPQ = 90o (angle in a semicircle)
also < PSQ + < SQP + < SPQ = 180o (angles in a triangle = 180o)
< PSQ + 38o + 90o = 190o
< PSQ = 128o = 180o
PSQ = 180o - 128o
PSQ = 52o
Similar Questions
Find the value of x at the minimum point of the curve y = x3 + x2 - x + 1 ...
Find the 8th term of the A.P -3, -1, 1 ...... ...
make u the subject in x =\(\frac{2u-3}{3u + 2}\)...
If tan x = \(\frac{3}{4}\), 0 < x < 90\(^o\), evaluate \(\frac{\cos x}{2 sin x}\) ...
Simplify \(\frac{6^{2n + 1} \times 9^n \times 4^{2n}}{18^n \times 2^n \times 12^{2n}}\)...
In the diagram, PQ and PS are tangents to the circle O. If PSQ = m, <SPQ = n and <SQR = 33\(^o...
If n(P) = 20 and n(Q) = 30 and n(PuQ) = 40, find the value n(PnQ) ...
G varies directly as the square of H, If G is 4 when H is 3, find H when G = 100 ...