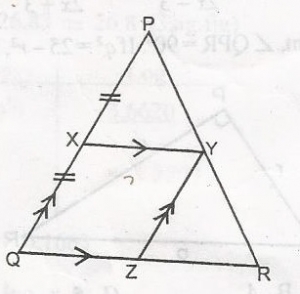
In the figure /PX/ = /XQ/, PQ//YZ and XV//QR. What is the ratio of the area of XYZQ to te area of \(\bigtriangleup\)YZR?
1:2
2:1
1:2
3:1
Correct answer is B
From the diagram, XYZQ is a parallelogram. Thus, |YZ| = |XQ| = |PX|; \(\bigtriangleup\)PXY, Let the area of XYZQ = A1, the area of \(\bigtriangleup\)PXY
= Area of \(\bigtriangleup\)YZR = A2
Area of \(\bigtriangleup\)PQR = A = A1 + 2A2
But from similarity of triangles
\(\frac{\text{Area of PQR}}{\text{Area of PXY}} = (\frac{PQ}{PX})^2 = (\frac{QR}{XY})^2\)
\(\frac{A}{A_2} = (\frac{2}{1})^2 = \frac{2}{1}\)
A = 4A2 But, A = A1 + 2A
A1 = 4A2 - 2A2
A1 = 2A2
\(\frac{A_1}{A_2}\) = 2
A1:A2 = 2:1
Area of XYZQ:Area of \(\bigtriangleup\)YZR = 2:1
Similar Questions
In the diagram, PR is a diameter of the circle PQRS. PST and QRT are straight lines. Find QRS ...
Simplify 1\(\frac{3}{4} - (2 \frac{1}{3} + 4)\)...
Given that logp = 2 logx + 3logq, which of the following expresses p in terms of x and q? ...
Approximate 0.9875 to 1 decimal place. ...
Given that t = \(2 ^{-x}\), find \(2 ^{x + 1}\) in terms of t. ...
A predator moves in a circle of radius √2 centre (0,0), while a prey moves along the line y = ...