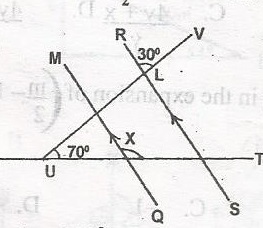
In the diagram, MQ//RS, < TUV = 70o and < RLV = 30o. Find the value of x
150o
110o
100o
95o
Correct answer is C
L + 30o - 180o(Sum of < s on straight line)
L = 180o - 30o = 150o
L = q = 150o(opposite < s are equal)
y = b = 30o(alt. < s)
b + c = 180o(sum of < s on str. line)
30o + c 180
c = 180 - 30
c = 150o
b = a = 30o (opp < s are equal)
c = d = 150o (opp < s are equal)
a + k + 70o = 180o (sum of < s on \(\bigtriangleup\))
30o + k + 70o = 180
k + 100o = 180
k = 180 - 100
k = 80o
x + 80o = 180(sum of < s on straight line)
x = 180o - 80o
x = 100o
Similar Questions
A sales boy gave a change of N68 instead of N72. Calculate his percentage error ...
Simplify; \(\sqrt{2}(\sqrt{6} + 2\sqrt{2}) - 2\sqrt{3}\)...
If sec\(^2\)θ + tan\(^2\)θ = 3, then the angle θ is equal to?...
Simplify and express in standard form \(\frac{0.00275 \times 0.0064}{0.025 \times 0.08}\)...
If \(\frac{3e + f}{3f - e}\) = \(\frac{2}{5}\), find the value of \(\frac{e + 3f}{f - 3e}\)...
Simplify \((\frac{1}{\sqrt{5} + \sqrt{3}} - \frac{1}{\sqrt{5} - \sqrt{3}}) \times \frac{1}...
If 27x = 9y. Find the value of \(\frac{x}{y}\)...
The determination of the matrix \(\begin{pmatrix} 1 & 3 & 3 \\ 4 & 5 & 6\\ 2 & 0...
Evaluate and correct to two decimal places, 75.0785 - 34.624 + 9.83 ...