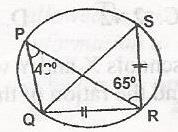
In the diagram, |SR| = |QR|. < SRP = 65o and < RPQ = 48o, find < PRQ
65o
45o
25o
19o
Correct answer is D
< RSQ = < RPQ = 48o (angle in the same segment)
< SQR < RSQ (Base angle of an isosceles \(\bigtriangleup\))
< SQR = 480
< QRS + < RSQ + < RSQ = 180o(sum of interior angles of a \(\bigtriangleup\))
i.e. < QRS + 48o + 48o = 180
< QRS = 180 - (48 + 48) = 180 - 96 = 84o
but < PRQ + < PRS = < QRS
< PRQ = < QRS - < PRS - 84 - 65
= 19o
Similar Questions
In the diagram, POS and ROT are straight lines. OPQR is a parallelogram, |OS| = |OT| and ∠O...
In the given diagram, \(\bar{QT}\) and \(\bar{PR}\) are straight lines, < ROS = (3n - 20), < S...
If 2\(^{a}\) = \(\sqrt{64}\) and \(\frac{b}{a}\) = 3, evaluate a\(^2 + b^{2}\) ...
Evaluate the following limit: \(lim_{x\to2} \frac {x^2 + 4x - 12}{x^2 - 2x}\)...
Simplify \(\frac{3x^3}{(3x)^3}\)...
The interior angles of a quadrilateral are (x + 15)°, (2x - 45)°, ( x - 30)° and (x...