In the figure below, /MX/ = 8cm, /XN/ = 12cm, /NZ/ = 4cm ...
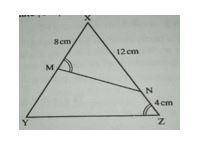
In the figure below, /MX/ = 8cm, /XN/ = 12cm, /NZ/ = 4cm and ∠ XMN = ∠ XZY. Calculate /YM/
32cm
24 cm
16 cm
12 cm
Correct answer is C
From the figure,
∠ XMN = ∠ XZY
Angle X is common
So, ∠ XNM = ∠ XYZ
Then from the angle relationship
\(\frac{XM}{XZ}\) = \(\frac{XN}{XY}\) = \(\frac{MN}{ZY}\)
XM = 8, XZ = 12 + 4 = 16,
XN = 12, XY = 8 + YM
\(\frac{8}{16}\) = \(\frac{12}{(8 + YM) }\)
Cross multiply
8(8 + YM) = 192
64 + 8YM = 192
8YM = 128
YM = \(\frac{128}{8}\)
= 16cm
Similar Questions
The locus of a point P which is equidistant from two given points S and T is ...
The figure is an example of the construction of a ...
If \(8^{x+1}=\frac{1}{4}\), find x...
The angle between the positive horizontal axis and a given line is 135°. Find the equation of th...
If 2x + 3y = 1 and x - 2y = 11, find (x + y) ...
Simplify: log6 + log2 - log12 ...
The angle of a sector of s circle, radius 10.5cm, is 48°, Calculate the perimeter of the se...