Find the value of the angle marked x in the diagram above...
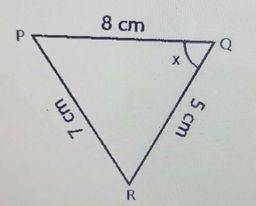
Find the value of the angle marked x in the diagram above
60\(^0\)
45\(^0\)
90\(^0\)
30\(^0\)
Correct answer is A
\(PR^2 = PQ^2 + RQ^2 - 2(PQ)(RQ)cos Q\)
\(\implies cos Q = \frac{PQ^2 + RQ^2 - PR^2}{2(PQ)(RQ)}\)
\(\implies cos Q = \frac{8^2 + 5^2 - 7^2}{2\times8\times5}\)
\(\implies cos Q = \frac{64 + 25 - 49}{80}\)
\(\implies cos Q = \frac{40}{80} = 0.5\)
\(\implies Q = cos^{-1} (0.5) = 60^0\)
\(\therefore x = 60^0\)
Similar Questions
If x is positive, for what range of values of x is 4 + 3x < 10?...
If a positive integer, list the values of x which satisfy the equation 3x - 4 < 6 and x - 1 > 0...
If x = 64 and y = 27, evaluate: \(\frac{x^{\frac{1}{2}} - y^{\frac{1}{3}}}{y - x^{\frac{2}{3}}}\)...
PQ and RS are two parallel lines. If the coordinates of P, Q, R, S are (1,q...
The shaded region above is represented by the equation ...
Evaluate \(\int^{\frac{\pi}{2}} _{\frac{-\pi}{2}} cos x dx\) ...