Find the volume of a cone which has a base radius of 5 cm...
Find the volume of a cone which has a base radius of 5 cm and slant height of 13 cm.
\(300\pi\) cm\(^3\)
\(325\pi\) cm\(^3\)
\(\frac{325}{3}\pi\) cm\(^3\)
\(100\pi\) cm\(^3\)
Correct answer is D
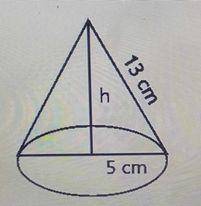
Volume of a cone = \(\frac{1}{3}\pi r^2 h\)
r = 5 cm
l = 13 cm
Using Pythagoras theorem
⇒ \(13^2 = 5^2 + h^2\)
⇒ \(169 = 25 + h^2\)
⇒ \(169 - 25 = h^2\)
⇒ \(h^2 = 144\)
⇒ \(h = \sqrt144 = 12 cm\)
∴ Volume of the cone = \(\frac{1}{3} \times\pi\times 5^2 x 12 = 100\pi\) cm\(^3\)
Similar Questions
In the diagram above, PQ is a tangent to the circle MTN at T. What is the size of ∠MTN? ...
Find the sum of the first twenty terms of the progression log a, log a2, log a3........
If y = x\(^2\) - x - 12, find the range of values of x for which y \( \geq \) 0 ...
Find the volume (in cm\(^3\)) of the solid shown above...
Simplify \(\frac{x - y}{x^{\frac{1}{3}} - x^{\frac{1}{3}}}\)...
Find the determinant of the matrix A = \(\begin{pmatrix} 2 & 3 \\ 1 & 3&...