A circle has a radius of 13 cm with a chord 12 cm away fr...
A circle has a radius of 13 cm with a chord 12 cm away from the centre of the circle. Calculate the length of the chord.
16 cm
8 cm
5 cm
10 cm
Correct answer is D
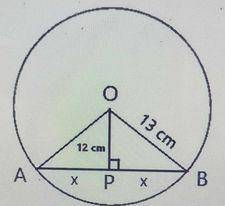
|AP| = |PB| = \(x\) (The perpendicular to a chord bisects the chord if drawn from the center of the circle.)
From ∆OPB
Using Pythagoras theorem
⇒ \(13^2 = 12^2 + x^2\)
⇒ \(169 = 144 + x^2\)
⇒ \(169 - 144 = x^2\)
⇒ \(x^2 = 25\)
⇒ \(x = \sqrt25 = 5 cm\)
∴ Length of the chord |AB| = \(x + x = 5 + 5 = 10 cm\)
Similar Questions
Given that 2p - m = 6 and 2p + 4m = 1, find the value of (4p + 3m). ...
Simplify: \(2\frac{1}{3} \div 2\frac{2}{3} \times 1\frac{1}{7}\)...
Express 302.10495 correct to five significant figures ...
If m : n = 2 : 1, evaluate \(\frac{3m^2 - 2n^2}{m^2 + mn}\)...
Simplify 2\(\sqrt{3}\) - \(\frac{6}{\sqrt{3}} + \frac{3}{\sqrt{27}}\)...
Evaluate \(^{n^2 + 1}\)C\(_{n+5}\) if n = 3 ...
In how many ways can the letters of the word TOTALITY be arranged? ...