In the diagram, O is the center of the circle QRS and&nbs...
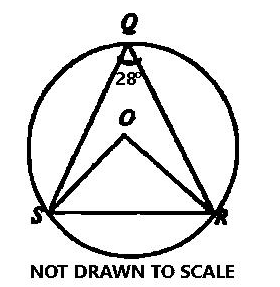
In the diagram, O is the center of the circle QRS and ∠SQR = 28°. Find ∠ORS.
\(56^0\)
\(28^0\)
\(76^0\)
\(62^0\)
Correct answer is D
∠SOR = 2 × 28° = 56° (angle at the centre is twice the angle at the circumference)
From ∆SOR
|OS| = |OR| (radii)
So, ∆SOR is isosceles.
∠ORS = \(\frac{180^0 - 56^0}{2} = \frac{124^0}{2}\) ( base angles of isosceles triangle are equal)
∴ ∠ORS = 62°
Similar Questions
The number of goals scored by a football team in 20 matches is shown in the table above What is...
A rectangle with width \(\frac{3}{4}\)cm and area 3 \(\frac{3}{8}\)cm\(^2\). Find the length...
Evaluate (25 × 4-2) ÷ (2-3 × 26)...
What must be added to 3x2 - 5x to make it a perfect square?...
If x * y = x + y2, find then value of (2*3)*5 ...
If P = 18, Q = 21, R = -6 and S = -4, Calculate \(\frac{(P- Q)^3 + S^2}{R^3}\) ...