Triangle OPQ above is the solu...
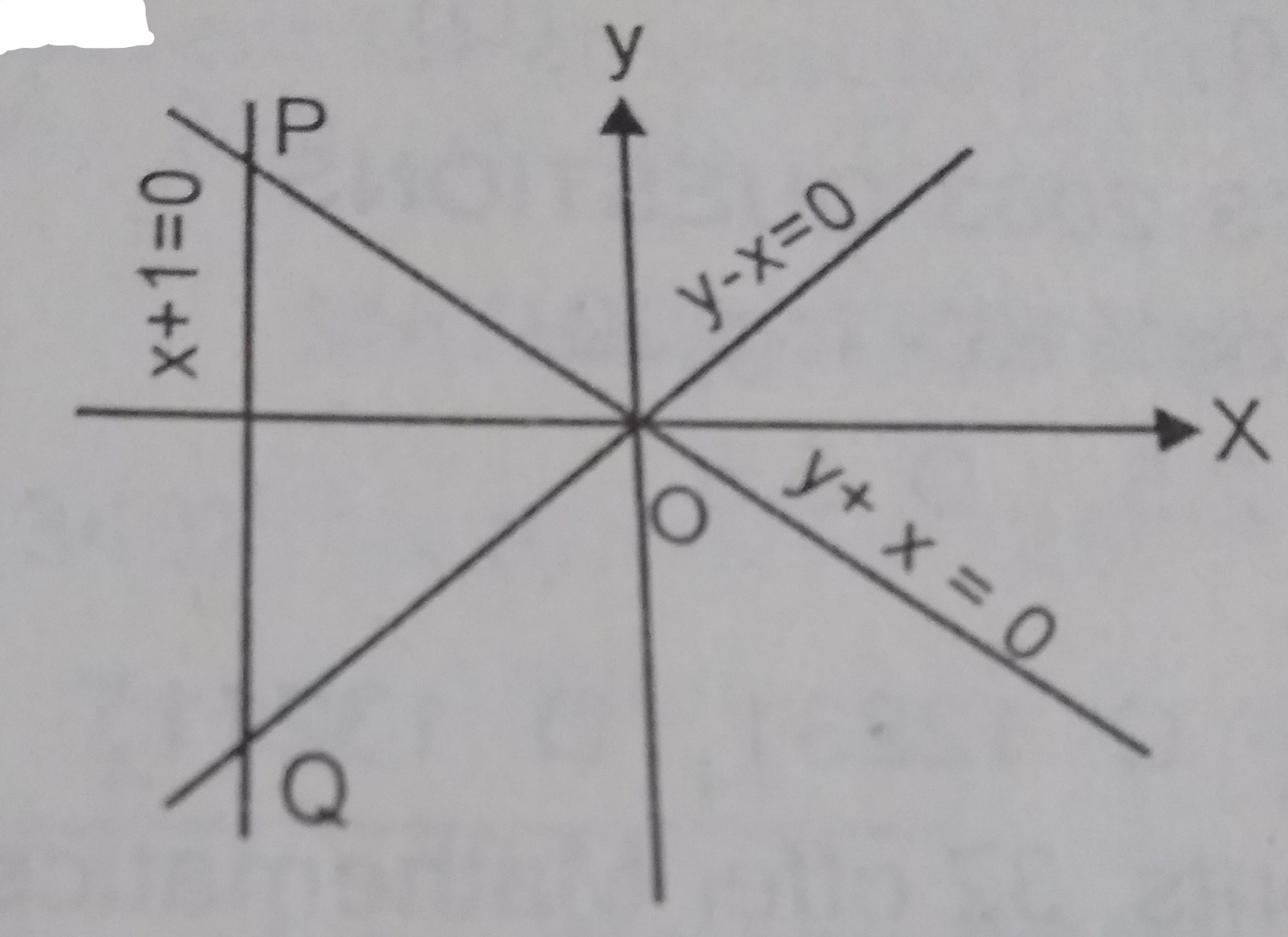
Triangle OPQ above is the solution of the inequalities
x + 1 ≥ 0, y + x ≤ 0, y - x ≥ 0
y + x ≤ 0, y - x ≥ 0, x -1 ≥ 0
x - 1 ≤ 0, y - x ≥ o, y + x ≥ 0
x - 1 ≤ 0, y + x ≤ 0, y - x ≤ 0
Correct answer is A
Lines bounding Δ OPQ
OQ; y - x = 0
y - x ≥ 0
PQ; x + 1 = 0
x + 1 ≥ = 0
PO; y + x = 0
y + x ≤ 0
∴ x + 1 ≥ 0, y + x ≤ 0, y - x ≥ 0
Similar Questions
Evaluate the following limit: \(lim_{x\to2} \frac {x^2 + 4x - 12}{x^2 - 2x}\)...
Find the mean of the numbers 1, 3, 4, 8, 8, 4 and 7 ...
Rationalize the denominator of the expression \(\frac{6 + 2\sqrt{5}}{4 - 3\sqrt{6}}\)...
If \(\frac {3 - \sqrt 3}{2 + \sqrt 3} = a + b\sqrt 3\), what are the values a and b?...
In the diagram, angle 20o is subtended at the centre of the circle, find the value of x...
What is the common ratio of the G.P. \((\sqrt{10} + \sqrt{5}) + (\sqrt{10} + 2\sqrt{5}) + ... \)?...
Without using table, calculate the value of 1 + sec2 30o...
If y = x2 - \(\frac{1}{x}\), find \(\frac{\delta y}{\delta x}\)...