In the diagram above, |PQ| = |PR| = |RS| and ∠RPS = 3...
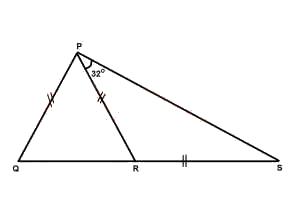
In the diagram above, |PQ| = |PR| = |RS| and ∠RPS = 32°. Find the value of ∠QPR
72o
64o
52o
32o
26o
Correct answer is C
From the figure, < PSR = 32° (base angles of an isos. triangle)
\(\therefore\) < PRS = 180° - (32° + 32°) = 116° (sum of angles in a triangle)
< QRP = 180° - 116° = 64° (angle on a straight line)
< PQR = 64° (base angles of an isos. triangle)
< QPR = 180° - (64° + 64°) = 52°
Similar Questions
Factorize 2e\(^2\) - 3e + 1 ...
Solve the simultaneous equations x + y = 2 and 3x - 2y = 1 ...
lf \(log_q p= r\), express p in terms of q and r...
Solve the equations m2 + n2 = 29 m + n = 7 ...
Evaluate: \((64^{\frac{1}{2}} + 125^{\frac{1}{3}})^2\)...
Evaluate \(\frac{1.25 \times 0.025}{0.05}\), correct to 1 decimal place...
In the diagram above, O is the center of the circle of radius 3.5cm, ∠POQ = 60o Use the...