In the diagram above, PQT is an isosceles triangle.|PQ| =...
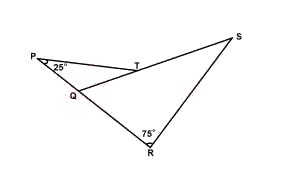
In the diagram above, PQT is an isosceles triangle.|PQ| = |QT|, ∠SRQ = 75°, ∠QPT = 25° and PQR is straight line. Find ∠RST
20o
50o
55o
70o
75o
Correct answer is C
< PTQ = 25° (base angles of an isos. triangle)
\(\therefore\) < PQT = 180° - (25° + 25°) = 130° (sum of angles in triangle PQT)
\(\therefore\) < RST = 130° - 75° = 55° (exterior angle = sum of 2 opp. interior angles)
Similar Questions
If the lines 2y - kx + 2 = 0 and y + x - k/2 = 0 Intersect at (1, -2), find the value of k...
Find the product of 0.0409 and 0.0021 leaving your answer in the standard form ...
Find the equation whose roots are 2 and \(-3\frac{1}{2}\)...
If two dice are thrown together, what is the probability of obtaining at least a score of 10? ...
Simplify \(\frac{3x^3}{(3x)^3}\)...
By how much is the mean of 30, 56, 31, 55, 43 and 44 less than the median? ...
In the diagram above, find x correct to the nearest degree ...