In the diagram, PQR is a tangent to the circle QST at Q. ...
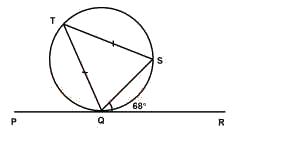
In the diagram, PQR is a tangent to the circle QST at Q. If |QT| = |ST| and ∠SQR = 68°, find ∠PQT.
34o
48o
56o
68o
73o
Correct answer is C
< STQ = < SQR = 68° (alternate segment)
\(\therefore\) < STQ = 68°
< TQS = \(\frac{180° - 68°}{2}\)
= \(\frac{112}{2} = 56°\)
\(\therefore\) < PQT = 180° - (68° + 56°)
= 180° - 124°
= 56°
Similar Questions
In the diagram, PX is a tangent to the circle and RST is an equilateral triangle. Calculate < PTS...
The locus of all points having a distance of 1 unit from each of the two fixed points a and b is...
Solve the equation 2a\(^2\) - 3a - 27 = 0...
If a = {x : 1 < x < 9} ; b = {x : 0 < x < 9} ; C = {x : 2 x < 9} and a, b, c U, what ...
\(\begin{array}{c|c} \text{Age in years} & 10 & 11 & 12 \\ \hline \text{Number of pupils...
If a rod 10cm in length was measured as 10.5cm, calculate the percentage error ...