In the diagram above, |QR| = 12cm and |QS| = 10cm. If &an...
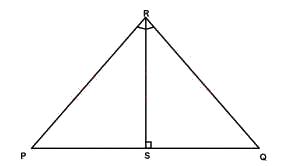
In the diagram above, |QR| = 12cm and |QS| = 10cm. If ∠PQR = 90°, ∠RSQ = 90° and PSQ is a straight line, find |PS|
3.3cm
4.4cm
5cm
5.5cm
6.6cm
Correct answer is B
\(\frac{PQ}{RQ} = \frac{RQ}{SQ}\) (Similar triangles)
\(\therefore \frac{PS + 10}{12} = \frac{12}{10}\)
\(10 (PS + 10) = 12 \times 12\)
\(10 PS + 100 = 144 \implies 10 PS = 44\)
\(PS = 4.4 cm\)
Similar Questions
Evaluate(111two)2 and leave your answer in base 2....
Simplify [1 ÷ (x + 1)] - [2 ÷ (x - 1)] + [3 ÷ (x2 - 1)]...
Evaluate \(\frac{1.25 \times 0.025}{0.05}\), correct to 1 decimal place...
Simplify 36\(^\frac{1}{2}\) x 64\(-^\frac{1}{3}\) x 5\(^0\) ...
Given that \(\frac{5^{n +3}}{25^{2n -3}}\) = 5º, find n...
In a triangle PQT, QR = \(\sqrt{3}cm\), PR = 3cm, PQ = \(2\sqrt{3}\)cm and PQR = 30°. Find angle...
The graph of y = \(ax^2 + bx + c\) is shown oon the diagram. Find the minimum value of y...