\(\frac{12}{7}\)cm
\(\frac{12}{7} \sqrt{6}\)cm
\(\frac{7}{12}\)cm
\(\frac{1}{2}\)cm
Correct answer is B
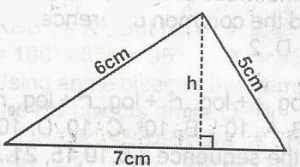
A\(\bigtriangleup\) = \(\sqrt{S(S - a) (S - b)(S - c)}\) (Hero's Formula)
S = \(\frac{a + b + c}{2}\) = \(\frac{5 + 6 + 7}{2}\)
\(\frac{18}{2} = 9\)
A\(\bigtriangleup\) \(\sqrt{9} \times 4 \times 3 \times 2\)
\(\sqrt{216} = 6 \sqrt{6}cm^3\)
A\(\bigtriangleup\) = \(\frac{1}{2} \times 6 \times h\)
6\(\sqrt{6} = \frac{1}{2} \times 7 \times h\)
h = \(\frac{12}{h} \sqrt{6}\)
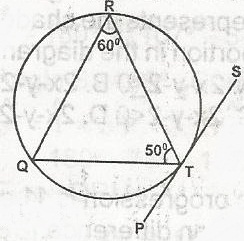
In the diagram, PTS is a tangent to the circle TQR at T. Calculate < RTS
120o
70o
60o
40o
Correct answer is B
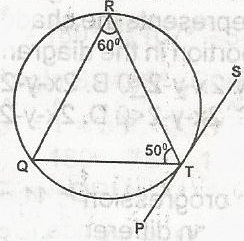
RTS = RQT (angle between a tangent and a chord at the point of contact is equal to the angle in the alternate segment) But R = Q + T = 180
RQT = 180o - (50 + 60)
= 180o - 110o
= 70o
Since RQT = RTS = 70o
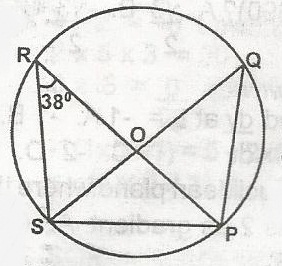
148o
104o
80o
52o
Correct answer is D
< SRP = < SQP = 38o (angle in the same segment of a circle are equal)
But < SPQ = 90o (angle in a semicircle)
also < PSQ + < SQP + < SPQ = 180o (angles in a triangle = 180o)
< PSQ + 38o + 90o = 190o
< PSQ = 128o = 180o
PSQ = 180o - 128o
PSQ = 52o
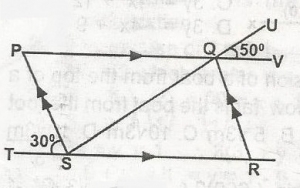
In the diagram, PQRS is a parallelogram. Find the value of < SQR
30o
50o
80o
100o
Correct answer is D
SQR + RQV + VQU = 18o angle on a straight line SP is parallel to QR and PV is parallel to TR
< STP = < RQV = 30o
But SQR + 30o + 50o = 180o
SQR = 180 - 80
= 100o
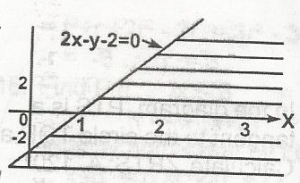
Find the inequality which represents the shaded portion in the diagram
2x - y - 2 \(\geq\) 0
2x - y - 2 \(\leq\) 0
2x - y - 2 < 0
2x - y - 2 > 0
Correct answer is A
2x - y - 2 \(\geq\) 0 = y \(\leq\) 2x - 2
when x = 0, y = -2, when y = 0, x = 1
JAMB Subjects
Aptitude Tests