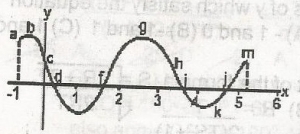
On the curve, the points at which the gradient of the curve is equal to zero are
c, d, f. i, l
b, e, g, j, m
a, b, c, d, f, i, j, l
c, d, f, h, i, l
Correct answer is B
The gradient of any curve is equal to zero at the turning points. i.e. maximum or minimum points. The points in the above curve are b, e, g, j, m
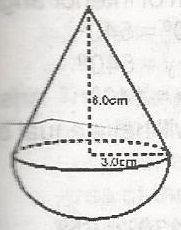
36\(\pi\)cm 3
54\(\pi\)cm 2
18\(\pi\)cm 2
108\(\pi\)cm 2
Correct answer is A
The volume of the solid = vol. of cone + vol. of hemisphere
volume of cone = \(\frac{1}{3} \pi r^2 h\)
= \(\frac{1 \pi}{3} \times (3)^2 x 6 = 18 \pi cm^2\)
vol. of hemisphere = \(\frac{4 \pi r^3}{6} = \frac{2 \pi r^3}{3}\)
= \(\frac{2 \pi}{3} \times (3)^3 = 18\pi cm^3\)
vol. of solid = 18\(\pi\) + 18\(\pi\)
= 36\(\pi\)cm3
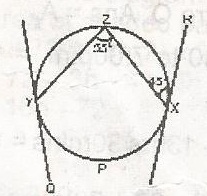
In the figure, XR and YQ are tangents to the circle YZXP if ZXR = 45° and YZX = 55°, Find ZYQ
135O
125O
100O
90O
Correct answer is A
< RXZ = < ZYX = 45O(Alternate segment)
< ZYQ = 90 + 45
= 135°
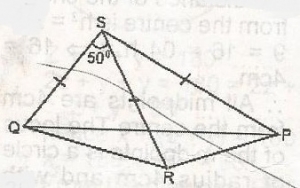
In the figure, PS = RS = QS and QRS = 50°. Find QPR
25O
40O
50O
65O
Correct answer is A
In the figure PS = RS = QS, they will have equal base QR = RP
In angle SQR, angle S = 50O
In angle QRP, 65 + 65 = 130O
Since RQP = angle RPQ = \(\frac{180 - 130}{2}\)
= \(\frac{50}{2} = 25^o\)
QPR = 25°
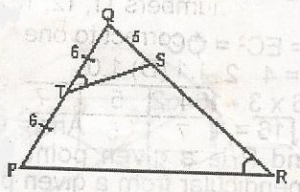
In the figure, STQ = SRP, PT = TQ = 6cm and QS = 5cm. Find SR
\(\frac{47}{5}\)
5
\(\frac{32}{5}\)
\(\frac{22}{5}\)
Correct answer is A
From similar triangle, \(\frac{QS}{QP} = \frac{TQ}{QR} = \frac{5}{12} = \frac{6}{QR}\)
QT = \(\frac{6 \times 12}{5} = \frac{72}{5} = SR = QR - QS\)
= \(\frac{72}{5} - 5 = \frac{72 - 25}{5}\)
= \(\frac{47}{5}\)
JAMB Subjects
Aptitude Tests