In the figure, PS = RS = QS and QRS = 50°. Find QPR
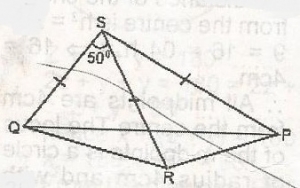
In the figure, PS = RS = QS and QRS = 50°. Find QPR
A.
25O
B.
40O
C.
50O
D.
65O
Correct answer is A
In the figure PS = RS = QS, they will have equal base QR = RP
In angle SQR, angle S = 50O
In angle QRP, 65 + 65 = 130O
Since RQP = angle RPQ = \(\frac{180 - 130}{2}\)
= \(\frac{50}{2} = 25^o\)
QPR = 25°
Similar Questions
If x = 64 and y = 27, evaluate: \(\frac{x^{\frac{1}{2}} - y^{\frac{1}{3}}}{y - x^{\frac{2}{3}}}\)...
In diagram, PQ || ST and < PQR = 120o, < RST = 130o, find the angle marked x ...
If the angle of a sector of a circle with radius 10.5 cm is 120°, find the perimeter of the sect...
Calculate the perimeter, in cm, of a sector of a circle of radius 8cm and angle 45o...