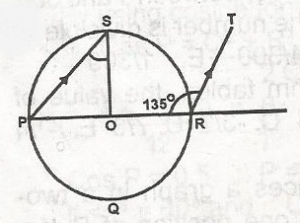
In the figure, O is the centre of circle PQRS and PS//RT. If PRT = 135, then PSO is
67\(\frac{1}{2}\)o
22\(\frac{1}{2}\)o
33\(\frac{1}{2}\)o
45o
90o
Correct answer is D
< R = 180o - 45o (sum of angles on a straight line)
< R = < P = 45o (corresponding angles)
< PSO = < P = 45o (\(\bigtriangleup\)PSO is a right angle)
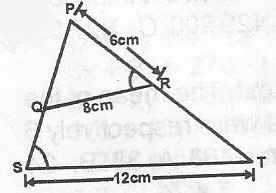
In the figure, TSP = PRQ, QR = 8cm, PR = 6cm and ST = 12cm. Find the length SP
4cm
16cm
9cm
14cm
Impossible, insufficient data
Correct answer is B
\(\frac{PQ}{6 + RT} = \frac{6}{12} = \frac{6}{PS}\)(Similar triangles)
\(\frac{6}{12} = \frac{8}{PS}\)
PS = \(\frac{12 \times 8}{6}\)
= 16cm
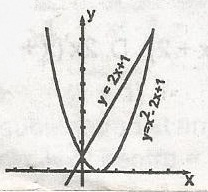
Find the x co-ordinates of the points of intersection of the two equations in the graph
1, 1
0, 4
0,0
4, 0
4, 9
Correct answer is D
If y = 2x + 1 and y = x2 - 2x + 1
then x2 - 2x + 1 = 2x + 1
x2 - 4x = 0
x(x - 4) = 0
x = 0 or 4
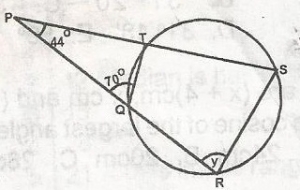
In the figure, determine the angle marked y
66o
110o
26o
70o
44o
Correct answer is A
From the diagram, < p = 44o, < Q = 70o
< y = 180o - (70 + 44o) = 66o
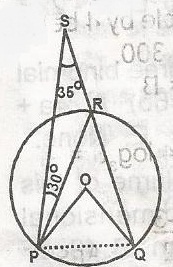
In the figure, QRS is a line, PSQ = 35o, SPR = 30o and O is the centre of the circle. Find OQP.
35o
30o
130o
25o
65o
Correct answer is D
< PSQ = 35o, < SPR = 30o
O is the centre of the circle, PRQ = 65o
< OQP = 90 - 65
= 25o
JAMB Subjects
Aptitude Tests