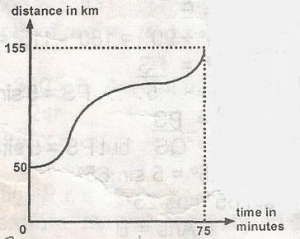
155km/hr
50km/hr
40km/hr
124km/hr
84km/hr
Correct answer is E
Distance = 155 - 50 = 105km
Time = 75mins
= \(\frac{75}{60}\)hr = \(\frac{5}{4}\)hr
Average speed = \(\frac{Distance}{time}\) = \(\frac{105}{\frac{5}{4}}\)
= \(\frac{105 \times 4}{5}\)
= 84km\h

In the diagram, angle QPR = 90o, angle PSR = 90o and PR = 5 units. Find the length of QS.
5 tan 25o sin 65o
5 cos 25o sin 65o
5 tan 25o cos 65o
cos 25o cos 65o
5 cosec 25o
Correct answer is C
From \(\bigtriangleup\)QPR, < R = 180o - (25o + 90o)
180o - 115o = 65o
From \(\bigtriangleup\)PSQ, Sin 65o = \(\frac{QPR}{hyp}\) = \(\frac{PS}{5}\)
PS = 5 sin 65o
From \(\bigtriangleup\)PSR, tan = \(\frac{OPP}{adj}\) = \(\frac{PS}{QS}\)
but PS = 5 sin 65o
QS tan 25o = PS
QS tan 25o = 5 sin 65o
QS = \(\frac{5 sin 65^o}{tan 25^o}\)
= 5 tan 25o cos 65o
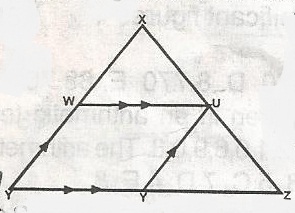
In the figure, WU//YZ, WY//YZ = 12cm, VZ = 6cm, XU = 8cm. Determine the length of WU.
1cm``3cm
6cm
2cm
4cm
Correct answer is D
From similar triangle, \(\frac{x}{6}\) = \(\frac{8}{12}\)
12x = 48
x = \(\frac{48}{12}\)
= 4
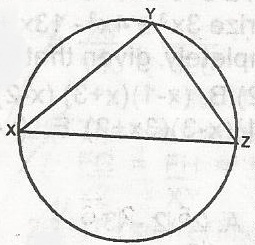
12cm2
28\(\frac{1}{2}\)cm2
16cm2
10cm2
6cm2
Correct answer is E
Area of the triangle XYZ = \(\frac{1}{2}\)bh = \(\frac{1}{2}\)ZY x XY
= \(\frac{1}{2}\) x 3 x 4
= 6cm2.
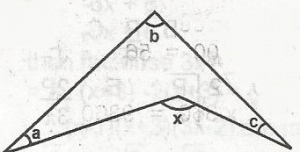
In the figure, find x in terms of a, b and c.
a + b + c
180o - (a + b + c)
a - b - c
a + b
a + c
Correct answer is A
180 - x + a + b + c
= 180(sum of interior angle in triangle)
a + b + c = x.
JAMB Subjects
Aptitude Tests