The locus of a point P which moves on one side only of a straight line XY so that ∠XPY = 90o is
a circle
a semicircle
an arc of a circle through X, Y
the perpendicular bisector of XY
Correct answer is B
No explanation has been provided for this answer.
3
4
6
7
Correct answer is A
Area of Trapezium = 1/2(sum of parralel sides) * ht
21 = 1/2(5 + 9)h
42 = 14h
h = 42/14
h = 3cm
6
7
8
9
Correct answer is D
\(S_n = 252, a = -16\hspace{1mm}and\hspace{1mm}l = 72\\S_n = \frac{n}{2}(-16+72)\\252 = \frac{n}{2}(-16+72)\\n=\frac{504}{56}\\n=9\)
Factorize completely 4abx - 2axy -12b2x + 6bxy
2x(a - 3b)(2b - y)
2x(3b - a)(2b - y)
2x(a - 3b)(y - 2b)
2x(2b - a)(3b - y)
Correct answer is A
4abx - 2axy - 12b2x + 6bxy = (4abx - 2axy) - (12b2x - 6bxy)
= 2ax(2b - y) -6bx(2b - y)
= (2ax - 6bx)(2b - y)
= 2x(a - 3b)(2b - y)
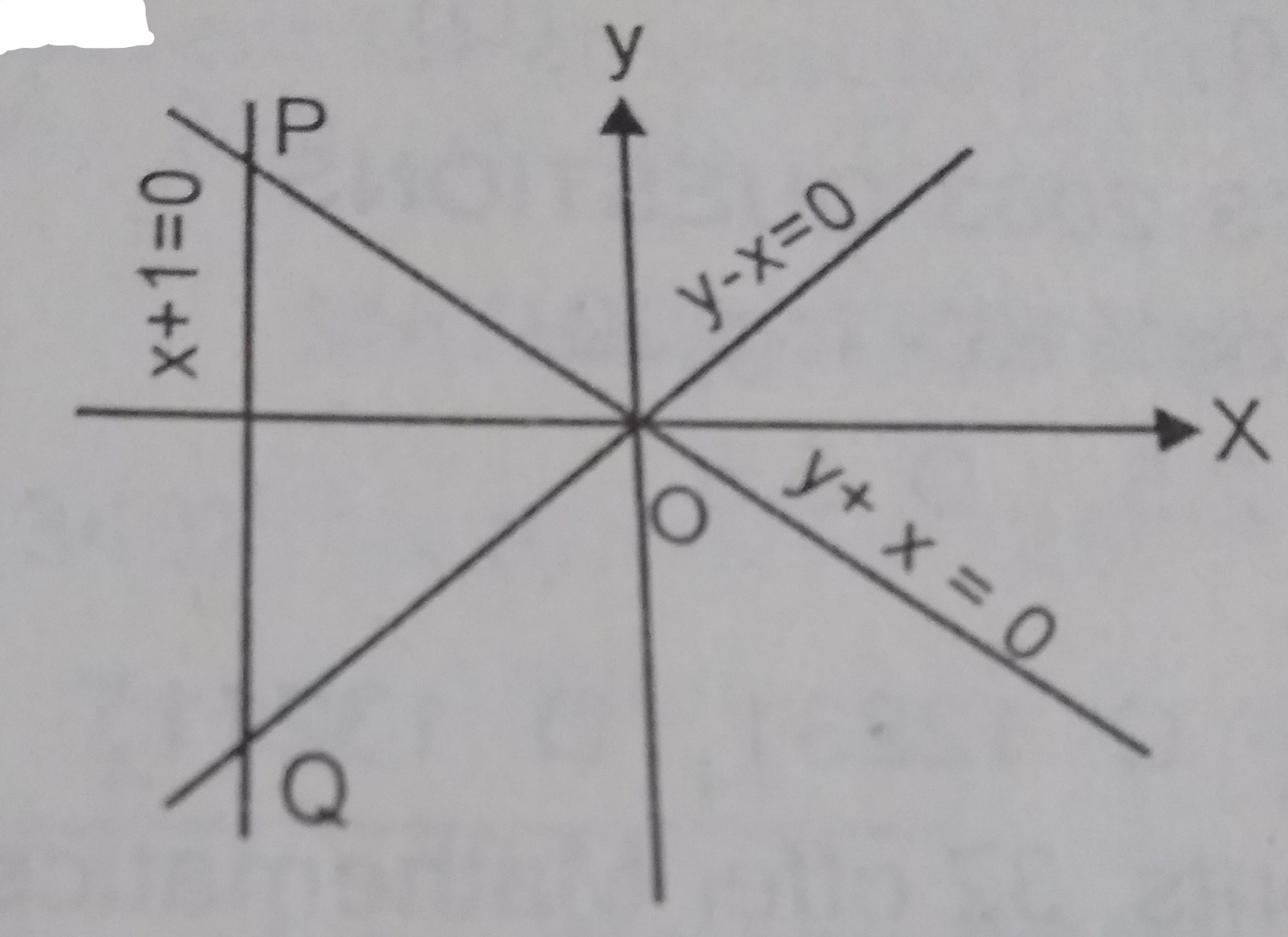
Triangle OPQ above is the solution of the inequalities
x + 1 ≥ 0, y + x ≤ 0, y - x ≥ 0
y + x ≤ 0, y - x ≥ 0, x -1 ≥ 0
x - 1 ≤ 0, y - x ≥ o, y + x ≥ 0
x - 1 ≤ 0, y + x ≤ 0, y - x ≤ 0
Correct answer is A
Lines bounding Δ OPQ
OQ; y - x = 0
y - x ≥ 0
PQ; x + 1 = 0
x + 1 ≥ = 0
PO; y + x = 0
y + x ≤ 0
∴ x + 1 ≥ 0, y + x ≤ 0, y - x ≥ 0
JAMB Subjects
Aptitude Tests