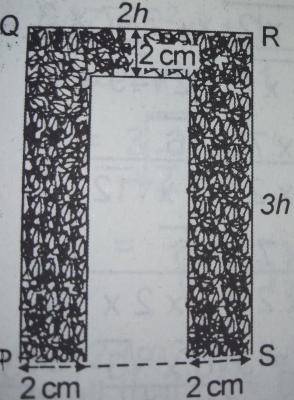
In the figure, PQRS is a rectangle. If the shaded area is 72 sq. cm, find h.
12cm
10cm
8cm
5cm
Correct answer is D
From the diagram, PQRS is a rectangle
Area of shaded part = 72sq.cm
But 72 = 3h - 4 + 6h - 4 + 4h
= 72 - 16h - 8
= 16h - 72 + 8
=16h = 80
h = \(\frac{80}{16}\)
= 5cm
Solve \(5^{2(x - 1)} \times 5^{x + 1} = 0.04\)
\(\frac{1}{3}\)
\(\frac{1}{4}\)
\(-\frac{1}{5}\)
\(-\frac{1}{3}\)
Correct answer is D
\(5^{2(x - 1)} \times 5^{x + 1} = 0.04\)
\(5^{2x - 2} \times 5^{x + 1} = 5^{-2}\)
\(2x - 2 + x + 1 = -2\)
\(3x - 1 = -2 \implies 3x = -2 + 1 = -1\)
\(x = -\frac{1}{3}\)
Subtract 16418\(_9\) from 18630\(_9\).
1121\(_9\)
2112\(_9\)
2113\(_9\)
2211\(_9\)
Correct answer is D
18630\(_9\) - 16418\(_9\) = 2211\(_9\)

I
II
III
IV
Correct answer is D
No explanation has been provided for this answer.
\(yx^2 = 300\)
\(yx^2 = 900\)
y = \(\frac{100x}{9}\)
\(y = 900x^2\)
Correct answer is B
Y \(\alpha \frac{1}{x^2} \rightarrow y = \frac{k}{x^2}\)
If x = 3 and y = 100,
then, \(\frac{100}{1} = \frac{k}{3^2}\)
\(\frac{100}{1} = \frac{k}{9}\)
k = 100 x 9 = 900
Substitute 900 for k in
y = \(\frac{k}{x^2}\); y = \(\frac{900}{x^2}\)
= \(yx^2 = 900\)
JAMB Subjects
Aptitude Tests