Express 495g as a percentage of 16.5kg
3%
3 \(\frac{1}{3}\)%
15%
30%
Correct answer is A
The two numbers must be expressed in the same unit. To convert 495g to kg, it will be divided by 1000
495g = \(\frac{495}{1000}\)
= 0.495kg
To express in percentage, 0.495 will be divided by 16.5 and then multiplied by 100
% will be added to the answer \(\frac{0.4950}{16.5}\) x 100
= 3%
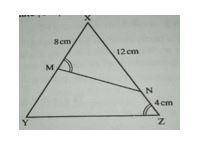
In the figure below, /MX/ = 8cm, /XN/ = 12cm, /NZ/ = 4cm and ∠ XMN = ∠ XZY. Calculate /YM/
32cm
24 cm
16 cm
12 cm
Correct answer is C
From the figure,
∠ XMN = ∠ XZY
Angle X is common
So, ∠ XNM = ∠ XYZ
Then from the angle relationship
\(\frac{XM}{XZ}\) = \(\frac{XN}{XY}\) = \(\frac{MN}{ZY}\)
XM = 8, XZ = 12 + 4 = 16,
XN = 12, XY = 8 + YM
\(\frac{8}{16}\) = \(\frac{12}{(8 + YM) }\)
Cross multiply
8(8 + YM) = 192
64 + 8YM = 192
8YM = 128
YM = \(\frac{128}{8}\)
= 16cm
In how many ways can the letters LEADER be arranged?
72
144
360
720
Correct answer is C
The word LEADER has 1L 2E 1A 1D and 1R making total of 6! \(\frac{6}{1!2!1!1!1!}\) = \(\frac{6!}{2!}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 \times 1}{2 \times 1}\)
= 360
Integrate the expression 6x\(^2\) - 2x + 1
3x\(^3\) - 2x\(^2\) + x + c
2x\(^3\) - x\(^2\) + x + c
2x\(^3\) – 3x\(^2\) + c
x\(^3\) + x\(^2\) – x + c
Correct answer is B
6x\(^2\) - 2x + 1
\(\frac{6x^{2+1}}{2+1} - \frac{2x^{1+1}}{1+1}+ 1x = \frac{6x^3}{3} - \frac{2x^2}{2} + x\)
\(2x^3 - x^2 + x + c\)
52cm
43cm
40cm
15cm
Correct answer is B
Tan 74 = 150/x x = 150/tan 74 = 43.01cm
JAMB Subjects
Aptitude Tests