Factorize completely X2+2XY+Y2+3X+3Y-18
(x + y + 6)(x + y -3)
(x - y - 6)(x - y + 3)
(x - y + 6)(x - y - 3)
(x + y - 6)(x + y + 3)
Correct answer is A
\(x^{2} + 2xy + y^{2} + 3x + 3y - 18\)
\(x^{2} + 2xy + 3x + y^{2} + 3y -18\)
\(x^{2} + 2xy - 3x + 6x + y^{2} -3y + 6y -18\)
\(x^{2} + 2xy -3x + y^{2} -3y + 6x + 6y -18\)
\(x^{2} + xy -3x + xy + y^{2} - 3y + 6x + 6y -18\)
x(x + y - 3) + y(x + y - 3) + 6(x + y - 3)
= (x + y - 3)(x + y + 6)
= (x + y + 6)(x + y -3)
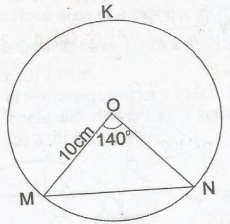
10cm
19cm
17cm
12cm
Correct answer is B
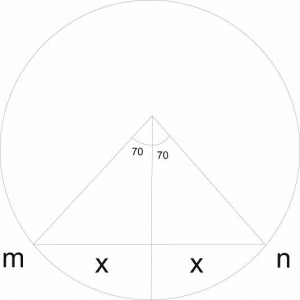
Find the diagram
Sin 70°
x = 10 Sin 70°
= 9.3969
Hence, length of chord MN = 2x
= 2 × 9.3969
= 18.79
= 19cm (nearest cm)
\(\frac{x_3}{3}\) - \(\frac{3x_2}{2}\) - 5x + k
\(\frac{x_3}{3}\) - \(\frac{3x_2}{2}\) + 5x + k
\(\frac{x_3}{3}\) + \(\frac{3x_2}{2}\) - 5x + k
\(\frac{x_3}{3}\) + \(\frac{3x_2}{2}\) + 5x + k
Correct answer is C
∫xndx = \(\frac{x_{n + 1}}{n + 1}\)
∫dx = x + k
where k is constant
∫(x2 + 3x − 5)dx
∫x2 dx + ∫3xdx − ∫5dx
\(\frac{2_{2 + 1}}{2 + 1}\) + \(\frac{3x^{1 + 1}}{1 + 1}\) − 5x + k
\(\frac{x_3}{3}\) + \(\frac{3x_2}{2}\) − 5x + k
Find the equation of the locus of a point p (x, y) such that pv = pw, where v= (1, 1) and w = (3, 5)
2x + 2y = 9
2x + 3y = 8
2x + y = 9
x + 2y = 8
Correct answer is D
The locus of a point p(x, y) such that pv = pw where v = (1, 1)
and w = (3, 5). This means that the point p moves so that its distance from v and w are equidistance
\(\sqrt{(x − x_1)^2 + (y − y_1)^2}\) = \(\sqrt{(x − x_2)^2 + (y − y_2)^2}\)
\(\sqrt{(x -1)^2 + (y - 1)^2}\) = \(\sqrt{(x - 3)^2 + (y - 5)^2}\)
square both sides
(x - 1)2 + (y - 1)2 = (x - 3)2 + (y - 5)2
x2 - 2x + 1 + y2 - 2y + 1 = x2 - 6x + 9 + y2 - 10y + 25
x2 + y2 -2x -2y + 2 = x2 + y2 - 6x - 10y + 34
Collecting like terms
x2 - x2 + y2 - y2 - 2x + 6x -2y + 10y = 34 - 2
4x + 8y = 32
Divide through by 4
x + 2y = 8
y is inversely proportional to x and y is 6 when x = 7. Find the constant of the variation
47
42
54
46
Correct answer is B
Y ∝ \(\frac{1}{2}\)
Y = 6, X = 7
Y = \(\frac{k}{x}\) where k is constant
6 = \(\frac{k}{7}\)
k = 42
JAMB Subjects
Aptitude Tests