In how many ways can the word MACICITA be arranged?
\(\frac{8!}{2!}\)
\(\frac{8!}{3! 2!}\)
\(\frac{8!}{2! 2! 2!}\)
8!
Correct answer is C
MACICITA is an eight letter word = 8!
Since we have repeating letters, we have to divide to remove duplicates accordingly. There are 2A, 2C, 2I
∴ \(\frac{8!}{2! 2! 2!}\)
₦ 35, 000
₦ 40,000
₦ 25,000
₦ 20,000
Correct answer is D
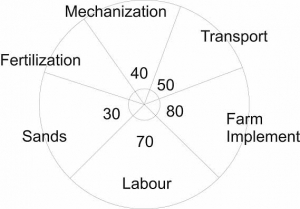
Total angle at a point = 3600
∴ To get the angle occupied by fertilizer we have,
40 + 50 + 80 + 70 + 30 + fertilizer(x) = 360
270 + x = 360
x = 360 - 270
x = 90
Total amount allocated to the farm
= ₦ 80,000
∴Amount allocated to the fertilizer
= \(\frac{\text{fertilizer (angle) × Total amount}}{\text{total angle}}\)
= \(\frac{90}{360}\) × 80,000
= ₦20,000
Find the principal which amounts to ₦ 5,500 at a simple interest in 5 years at 2% per annum
₦ 4,900
₦ 5,000
₦ 4,700
₦ 4,000
Correct answer is B
Principal = P, Simple Interest = I, Amount = A
Amount = Principal + Simple Interest
I = \(\frac{PRT}{100}\)
R = rate, T = time
I = \(\frac{P \times 5 \times 2}{100}\)
I = \(\frac{10P}{100}\)
I = \(\frac{P}{10}\)
Amount A = P + I
5500 = P + \(\frac{P}{10}\)
Multiply through by 100
5500 = 10P + P
5500 = 11P
p = \(\frac{5500}{11}\)
p = ₦5000
If a rod 10cm in length was measured as 10.5cm, calculate the percentage error
5%
5%
8%
7%
Correct answer is A
Actual measurement = 10cm
approximated value of measurement = 10.5cm
% error = \(\frac{\text{Actual measurement − Approximated}}{\text{Actual measure}}\) × 100
= \(\frac{10 − 10.5}{10}\) × 100
= \(\frac{-0.5}{10}\) × 100
ignore -sign i.e take absolute value
= \(\frac{0.5}{10}\) × 100
= 5 %
Evaluate \(\frac{0.00000231}{0.007}\) and leave the answer in standard form
3.3 x 10-4
3.3 x 10-3
3.3 x 10-5
3.3 x 10-8
Correct answer is A
\(\frac{0.00000231}{0.007}\) to standard form
= \(\frac{231 \times 10^{-8}}{7 \times 10^{-3}}\)
= 33 × 10\(^{-8 − (−3)}\)
= 33 × 10\(^{− 8 + 3}\)
= 33 × 10-5
= 3.3 x 10^-4
JAMB Subjects
Aptitude Tests