Given m = N\(\sqrt{\frac{SL}{T}}\) make T the subject of the formula
\(\frac{\text{NSL}}{M}\)
\(\frac{N^2SL}{M^2}\)
\(\frac{N^2SL}{M}\)
\(\frac{NSL}{M^2}\)
Correct answer is B
M = N \(\sqrt{\frac{SL}{T}}\),
make T subject of formula square both sides
M\(^{2}\) = \(\frac{N^2SL}{T}\)
TM\(^{2}\) = N\(^{2}\)SL
T = \(\frac{N^2SL}{M^2}\)
Evaluate 1 - (\(\frac{1}{5}\) x \(\frac{2}{3}\)) + ( 5 + \(\frac{2}{3}\))
4
3
2\(\frac{2}{3}\)
\(\frac{98}{15}\)
Correct answer is D
No explanation has been provided for this answer.
24oC
20oC
34oC
30oC
Correct answer is A
t ∝ h, t = 20, h
t = ? h = 60
t = kh where k is constant
20 = 50k
k = \(\frac{20}{50}\)
k = \(\frac{2}{5}\)
when h = 60, t = ?
t = \(\frac{2}{5}\) × 60
t = 24oC
If y = x Sin x, find \(\frac{dy}{dx}\) when x = \(\frac{\pi}{2}\)
\(\frac{- \pi}{2}\)
-1
1
\(\frac{ \pi}{2}\)
Correct answer is C
y = xsinx
\(\frac{dy}{dx}\) = \(1 \sin x + x \cos x\)
= \(\sin x + x \cos x\)
At x = \(\frac{\pi}{2}\)
= sin\(\frac{\pi}{2}\) + \(\frac{\pi}{2} \cos {\frac{\pi}{2}}\)
= 1 + \(\frac{\pi}{2}\) × 0
= 1

Evaluate (\(\sin\)45º + \(\sin\)30º ) in surd form
\(\frac{\sqrt{3}}{2\sqrt{2}}\)
√3 − \(\frac{1}{2}\)
\(\frac{1}{2}\)√2
1 + \(\frac{\sqrt{2}}{2}\)
Correct answer is D
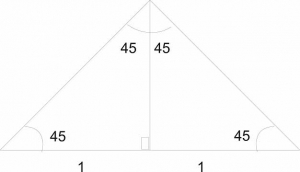
hypotenuse
sin = \(\frac{1}{2}\)
\(\sin45 = \frac{1}{\sqrt{2}}\)
= \(\frac{2}{2}\)
∴ (sin45 + sin30)
= \(\frac{1}{\sqrt{2}} + \frac{1}{2}\)
= \(\frac{\sqrt{2}}{2}\) + \(\frac{1}{2}\)
= \(\frac{\sqrt{2} + 1}{2}\)
= \(\frac{1 + \sqrt{2}}{2}\)
JAMB Subjects
Aptitude Tests