Given that n(p) = 19, m(P \(\cup\) Q) = 38 and n(P \(\cap\) Q) = 7, Find n(C)
26
31
36
50
Correct answer is A
n(P \(\cup\) Q) = m(P \(\cap\) C)
38 = 19 = n(C) - 7
n(C) = 38 - 12
= 26
G varies directly as the square of H, If G is 4 when H is 3, find H when G = 100
15
25
75
225
Correct answer is A
G \(\alpha\) H2
G = KH2
4 = K(3)2
4 = 9k; K = \(\frac{4}{9}\)
100 = \(\frac{4}{9}H^2\)
4H2 = 900
H2 = \(\frac{900}{4}\)
H2 = 225
H = \(\sqrt{225}\)
H = 15
If \(\sqrt{72} + \sqrt{32} - 3 \sqrt{18} = x \sqrt{8}\), Find the value of x
1
\(\frac{3}{4}\)
\(\frac{1}{2}\)
\(\frac{1}{4}\)
Correct answer is C
\(\sqrt{2} + \sqrt{32} - 3\sqrt{18} = x\sqrt{8}\)
= \(\sqrt{36 \times 2} + \sqrt{16 \times 2} - 3\sqrt{2 \times 9}\)
= x\(\sqrt{2 \times 4}\)
= 6\(\sqrt{2} + 4\sqrt{2} - 9\sqrt{2} = 2 \times \sqrt{2}\)
\(\sqrt{2} (6 + 4 - 9) = 2x\sqrt{2}\)
\(\sqrt{2} = 2x \sqrt{2}\) divide both sides by \(\sqrt{2}\)
\(\frac{\sqrt{2}}{\sqrt{2}} = \frac{2 \times \sqrt{2}}{\sqrt{2}}\)
1 = 2x
2x = 1
x = \(\frac{1}{2}\)
Simplify \(\frac{m}{n} + \frac{(m - 1)}{5n} = \frac{(m - 2)}{10n}\) where n \(\neq\) 0
\(\frac{m - 3}{10n}\)
\(\frac{11m}{10n}\)
\(\frac{m + 1}{10n}\)
\(\frac{11m + 4}{10n}\)
Correct answer is B
\(\frac{m}{n} + \frac{(m - 1)}{5n} - \frac{(m - 2)}{10n}\); \(\frac{10m + 2(m - 1) - 1(m - 2)}{10m}\)
= \(\frac{10m + 2m - 2 - m + 2}{10n}\)
= \(\frac{10m + 2m - m - 2 + 2}{10n}\)
= \(\frac{11m}{10n}\)
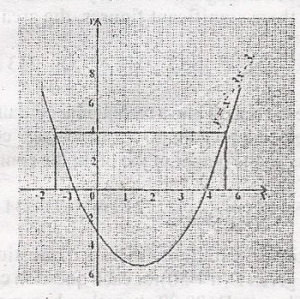
The graph represents the relation y = xo2 - 3x - 3. Find the value of x for which x2 - 3x = 7
-1.55, 4.44
1.55, -4.55
-1.55, -4.55
1.55, 4.55
Correct answer is A
x2 - 3x = 7
x2 - 3x - 7 = 0
What can you add to both sides of the equation to give the same value of y = x2 - 3x - 3
The number is 4
x2 - 3x - 7 + 4 = 4
x2 - 3x - 3 = 4
but y = x2 - 3x - 3
y = 4; So are y = 4 draw a line parallel to x axis, to cut or intersect the graph. At these points look down to see the corresponding values on x axis
This give -1.55 and 4.55
WAEC Subjects
Aptitude Tests